Вы находитесь в разделе Типовых решений систем безопасности
Оценка местоположения источника радиоизлучения в условиях априорной неопределенности ошибок измеренийВ.И. Гныря Ю.Д. Ильин Обработка измерений в системах местоопределения В системе место определения связь м. результатами измерений
Требуется найти оценку вектора параметров местоположения Решение системы (1) состоит в том, что стараются выбрать (подогнать) значения неизвестных параметров X так, чтобы совокупность остаточных невязок обладала какими-то экстремальными св. Для этого составляется некоторый функционал Обычно в задачах оценки местоположения ИРИ наиболее употребительны так называемые М-оценки [1]:
где L - весовая функция, определяющая метод оценивания. При нормальном распределении ошибок Устойчивые процедуры оценки местоположения ИРИ К сожалению, характеристики оптимальных процедур обработки во множественных случаях могут резко ухудшаться даже при сравнительно малых отклонениях от исходных предположений. Поэтому необходимо строить робастные (устойчивые) алгоритмы обработки, значит алгоритмы, которые обладают высокой эффективностью в условиях, когда характеристики распределений ошибок меняются в пределах заданных классов. Робастная процедура должна обладать следующими св [1]:
Ключевая идея робастного оценивания, которая относительно просто вписывается в состав существующих алгоритмов и программ, заключается в следующем: допустим, что по наблюдениям Пусть Si - некоторая оценка или априорное значение среднеквадратической ошибки (СКО) наблюдений Метрически винзоризуются наблюдения заменой псевдонаблюдениями:
Константой Ci регулируется степень робастности. Далее по псевдонаблюдениям (3) вычисляются новые значения X(i) с помощью МНК (2), действия повторяются до достижения сходимости. Минимаксный подход Хьюбера предполагает, что оптимальная оценка будет не хуже, чем в случае "наименее благоприятной" плотности. Решающее правило строится на определении такой плотности, которая минимизирует информацию по Фишеру. В случае
где F0 - функция, описывающая основную долю измерений,
Пусть изучим один из способов обработки измерений, который основывается на усреднении результатов обработки, полученных несколькими способами: МНК, который является оптимальным в случае гауссовского распределения ошибок, и МНМ, который проявляет оптимальные свойства при лапласовском распределении или при редких выбросах (4), что равносильно [1].
Допустим, что по выборке X1 - оценка МНК и Х2 - оценка МНМ. В [2] показано, что оценка с минимальной дисперсией является единственной. Поэтому алгоритм окончательной оценки будет выглядеть следующим образом:
Приведем так же один из способов, известных как методы с отбраковкой, которые являются в какой-то степени робастными. Этот способ представляет собой переформулировку алгоритма (5). Необходимо выбрать такие измерения из Пусть На основе статистического моделирования азимутальной системы местоопределения при Читайте далее:  "Летающие" купола, или рельсовые подвесные системы для камер видеонаблюдения "Летающие" купола, или рельсовые подвесные системы для камер видеонаблюдения Особенности агресс. маркетинга рынка B2B Особенности агресс. маркетинга рынка B2B Награды Национальной отраслевой премии "За укрепление безопасности России" "ЗУБР 2007" Награды Национальной отраслевой премии "За укрепление безопасности России" "ЗУБР 2007" Активные микрофоны для систем видеонаблюдения Активные микрофоны для систем видеонаблюдения Отрасль безопасности с размахом отметила свой праздник Отрасль безопасности с размахом отметила свой праздник Предвестники эпохи 1Р-видеонаблюдения Предвестники эпохи 1Р-видеонаблюдения Риф Стринг-202 Риф Стринг-202 Российский рынок безопасности евростандарта Российский рынок безопасности евростандарта Событие мирового масштаба в области безопасности: IFSEC упрочняет свои позиции Событие мирового масштаба в области безопасности: IFSEC упрочняет свои позиции АРД-объективы с фокусным расстоянием 2,8 мм и креплением типа CS-mount АРД-объективы с фокусным расстоянием 2,8 мм и креплением типа CS-mount Тест: электромагнитные замки российского производства Тест: электромагнитные замки российского производства Тест: IP-видеокамеры низкой ценовой категории Тест: IP-видеокамеры низкой ценовой категории Трал Трал ЗУБР-2007: новые горизонты ЗУБР-2007: новые горизонты
|

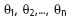 и вектором местоположения ИРИ
и вектором местоположения ИРИ  описывается следующей системой уравнений:
описывается следующей системой уравнений: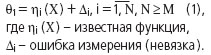
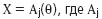 , задается конечным алгоритмом.
, задается конечным алгоритмом.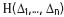 от невязок и минимизируется в пространстве неизвестных параметров X.
от невязок и минимизируется в пространстве неизвестных параметров X.
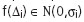 оптимальным решением (2) является метод наименьших квадратов (МНК) L = (z)2. В случае лапласовского распределения ошибок L = z задача решается с помощью оценки по методу наименьших модулей (МНМ). Если известны законы распределения невязок, оценка называется оценкой по методу максимального правдоподобия (ММП) L = log f(z).
оптимальным решением (2) является метод наименьших квадратов (МНК) L = (z)2. В случае лапласовского распределения ошибок L = z задача решается с помощью оценки по методу наименьших модулей (МНМ). Если известны законы распределения невязок, оценка называется оценкой по методу максимального правдоподобия (ММП) L = log f(z).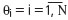 , N сделана подгонка по МНМ и в результате получено значение X(0) - вектора местоположения. Затем вычисляются остатки:
, N сделана подгонка по МНМ и в результате получено значение X(0) - вектора местоположения. Затем вычисляются остатки: 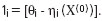 .
.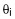 , (или, что так же лучше, стандартных ошибок остатков li ).
, (или, что так же лучше, стандартных ошибок остатков li ).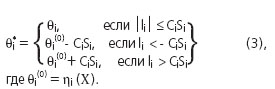
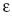 загрязненного нормального распределения важнейшей модели реальных ситуаций:
загрязненного нормального распределения важнейшей модели реальных ситуаций: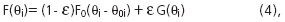 ,
, - доля загрязнений,
- доля загрязнений, 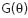 - неизвестная функция распределения. Ci связано с
- неизвестная функция распределения. Ci связано с 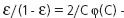 , где
, где 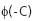 - нормальное распределение,
- нормальное распределение, 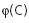 - плотность нормального распределения.
- плотность нормального распределения.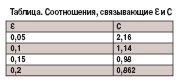
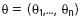 получены:
получены: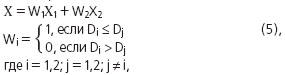
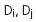 - выборочные дисперсии оценок по алгоритмам МНК и МНМ.
- выборочные дисперсии оценок по алгоритмам МНК и МНМ.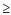 3), которые давали бы максимальную точность.
3), которые давали бы максимальную точность.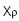 - оценки, полученные по выборкам размера
- оценки, полученные по выборкам размера 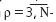 по алгоритму, допустим, МНК (МНМ), желателен такой вектор измерений
по алгоритму, допустим, МНК (МНМ), желателен такой вектор измерений 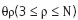 из набора
из набора 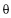 и соответственно
и соответственно  и
и 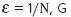 - загрязняющего распределения получено, что МНК является неустойчивойпроцедурой, МНМ - устойчивой (робастной), а эффективной - алгоритм (5).
- загрязняющего распределения получено, что МНК является неустойчивойпроцедурой, МНМ - устойчивой (робастной), а эффективной - алгоритм (5).