Раздел: Документация
0 ... 9 10 11 12 13 14 15 ... 49 где /—частота напряжения питающей Cwh; f1=mf—частота первой гармоники пульсации. Например,-при частоте питающей сети /=50 Гц частота первой гармоники пульсации (и— 1) будет иметь следующие значения: а) 100 Гц для однофазной мостовой схемы (т = 2); - б) 150 Гц для трехфазной схемы с нулевым выводом {т = 3); в) 300 Гц для трехфазной мостовой схемы (т = 6). Амплитуда и-й гармоники напряжения для схем, работающих с углом управления а = 0, определяется по формуле [10] Unm=Ud2/(m2n2-l).(2.82) Согласно (2.82) самое большое значение имеет амплитуда первой гармоники (и=1), а остальные убывают обратно пропорционально квадрату порядкового номера гармонической составляющей. Действующее значение переменной составляющей выпрямленного напряжения можно выразить формулой и=1ип,(2.83) V п=1 где Un — действующее значение и-й гармонической составляющей. На практике пульсация или содержание переменной составляющей в выпрямленном напряжении оценивается значением коэффициента пульсаций кп. Существуют различные определения коэффициента пульсаций кп, использование которых зависит от типа измерительной аппаратуры и требований, предъявляемых, к источнику выпрямленного напряжения. Наиболее распространенными из этих определений являются следующие: kn=Ulm/Ud; d, max d, min . k=- k:= 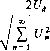 (2.84) где Ulm — амплитуда первой гармоники выпрямленного напряжения; udtmax, mdmin — максимальное и минимальное мгновенные значения выпрямленного напряжения. Разница в значениях коэффициентов пульсаций будет тем меньше, чем более сглаженным является выпрямленное на- пряжение. Например, для трехфазной мостовой схемы fcn = 5,7%; kn = 7%; A:J = 4,2%. Задержка подачи на тиристоры управляющих импульсов относительно моментов естественной коммутации на угол а приводит к изменению гармонических составляющих в выпрямленном напряжении. Из диаграмм выпрямленного напряжения, приведенных для рассмотренных схем, видно, что с ростом угла а увеличивается переменная составляющая (пульсация растет). В то же время период повторяемости пульсаций не зависит от угла а. При условии непрерывности выпрямленного тока id (что соответствует наиболее распространенному режиму работы с активно-индуктивной нагрузкой) зависимость между амплитудами гармонических составляющих и углом управления а одинакова для различных схем и дается формулой [13] Unm = Uю cos а 2/(от 2п 2 - 1) v/l+m2«2tga, (2.85) где Ud0—среднее значение выпрямленного напряжения при ос = 0. Формула (2.85) является частным случаем формулы (2.82), когда а = 0. Из рассмотренных принципов действия схем выпрямления следует, что они в большинстве случаев потребляют из питающей сети несинусоидальный ток. Так, однофазный двух-полупериодный выпрямитель при активной нагрузке и а=0 потребляет синусоидальный ток (см. рис. 2.5) и высшие гармоники тока равны нулю, а при акгивно-индуктивной нагрузке, когда <»Ld = oo, ток имеет прямоугольную форму (см. рис. 2.8) и может б&ть представлен в виде суммы гармонических составляющих "<9>=§ sin 0+~ sin 3$ + ...+-sin n 0 3n (2.86) Из (2.86) видно, что в первичный ток двухполупериодной схемы (т = 2) входят только нечетные гармоники. Это следует из общего закона для порядка высших гармонических составляющих первичного тока," по которому п = кт±1, где к= 1, 2, 3... Согласно этому закону потребляемый ток содержит, помимо основной гармоники (первой), высшие, наименьший номер которых тем выше, чем больше кратность пульсации выпрямленного напряжения т. Если учесть, что амплитуды гармонических составляющих 1пт связаны с амплитудой основной (первой) гармоники 11т соотношением I„m = hm/n, то увидим, что с увеличением числа фаз схемы выпрямления (с увеличением числа т) потребляемый из сети ток приближается к синусоидальному (так как содержание высших гармоник уменьшается). Снижение содержания высших "гармоник в первичном токе в ряде случаев бывает необходимым, так как они вызывают дополнительные потери и искажают форму кривой питающего напряжения. Особенно заметно эти эффекты проявляются при соизмеримости мощностей источника переменного тока и выпрямителя. Гармонический состав тока, потребляемого из сети управляемым выпрямителем, существенно зависит от характера нагрузки. Если нагрузка активная или активно-индуктивная, но не обеспечивается режим работы с непрерывным током id, то с ростом угла а происходит увеличение амплитуд высших гармоНик потребляемого тока (при условии неизменности амплитуды первой гармоники). При активно-индуктивной нагрузке и идеально сглаженном выпрямленном токе {юЬл — оо) угол управления а не оказывает влияния На гармонический состав потребляемого тока. Следует отметить, что данный вывод справедлив при допущении о равенстве нулю индуктивных сопротивлений обмоток трансформаторов. 2.3. КОММУТАЦИЯ И РЕЖИМЫ РАБОТЫ ВЫПРЯМИТЕЛЕЙ 2.3.1. КОММУТАЦИЯ ТОКОВ В СХЕМАХ ВЫПРЯМЛЕНИЯ В § 2.2 процесс перехода тока с одного тиристора на другой (процесс коммутации) рассматривался как мгновенный. В реальных схемах из-за наличия в цепи переменного тока индуктивных сопротивлений, в частности индуктивных сопротивлений обмоток трансформатора, обусловленных в основном потоками рассеяния в магнитной системе трансформатора, процесс коммутации имеет определенную длительность. Эти сопротивления определяются из опыта короткого замыкания вторичных обмоток трансформатора и при анализе схем учитываются в виде общих (для каждой фазы) эквивалентных индуктивностей ls, представляющих собой суммарную индуктивность вторичной обмотки и приведенную по числу витков индуктивность первичной обмотки (см. § 1.1). Помимо индуктивного сопротивления на процессы коммутации влияет и активное сопротивление обмоток, но его влияние в нормальных режимах работы значительно меньше. Поэтому рассматриваем процессы коммутации с учетом только индуктивных сопротивлений обмоток, полагая при этом выпрямленный ток идеально сглаженным (co£d = oo). Учитывая одинаковый характер процессов коммутации в различных схемах, остановимся на наиболее простой схеме выпрямления— однофазной двухполу-периодной. На рис. 2.25 представлены эквивалентная схема однофазного двухполупериодного выпрямителя на тиристорах и диаграммы напряжений и токов, поясняющие процесс коммутации токов. Индуктивные сопротивления обмоток учтены введением в схему индуктивностей ls. Предположим, что в проводящем состоянии находится тиристор vs,. В момент поступает управляющий импульс на тиристор vs2. > Поскольку потенциал анода тиристора в этот момент положителен относительно катода, тиристор включается. Начиная с момента 9Х оба тиристора будут включены, и вторичные полуобмотки трансформатора оказываются  Рис. 2.25. Процесс коммутации тиристоров в однофазном двухполупериод- ном выпрямителе: а—эквивалентная схема выпрямителя, б— диаграммы напряжений , и токов замкнутыми через них накоротко. Под воздействием ЭДС вторичных полуобмоток ёа и еь в короткозамкнутой цепи (контуре коммутации) возникает ток короткого замыкания /к, который является коммутирующим током. Этот ток можно в любой момент времени, начиная с Эь определить как сумму -двух составляющих—установившейся iK и свободной 4, которые рассчитываются по следующим соотношениям: ;l 2j2 2х, t/2cos(9--a); i, = 2£/, 1 cos а, (2,87) (2.88) 2—действующее значение напряжения вторичной полуобмотки; хг — (дЬ5. Результирующий ток короткого замыкания с учетом (2.87) и (2.88) можно записать в виде Fiu к = й + Ц = *—- [cos а - cos (а+9)]. (2.89) Этот ток направлен от полуобмотки Ъ с большим потенциалом к полуобмотке а с меньшим потенциалом (на рис. 2.25 указано направление тока i% при включении тиристора VSy и выключении тиристора VSi). Учитывая, что выпрямленный ток id при (nLd — <x> в период коммутации остается неизмененным, можно записать для узла О или О следующее уравнение токов: ivsi -HVs2 = /</ = const,(2.90) где Id—среднее значение выпрямленного тока или тока нагрузки. Уравнение (2.90) справедливо для любого момента времени. Пока ток проводит только тиристор VS\, получаем ivsi = Id и iys2=0. На интервале одновременной проводимости тиристоров VS] и VS: (интервал коммутации тока с тиристора VSi на тиристор VS?) ivsi = Id — i* и ivsi = i*. Когда ток будет проводить только шристор VS:, получим: ivs2 = h, Ivsi—Q- Из рис. 2.25 видно, что в интервале от 9i до Э2 ток iVS2 плавно увеличивается, a ivs2 уменьшается. Когда ток iyS2 станет равным U, а ток ivsi снизится до нуля, тиристор VSi выключится и ток нагрузки будет продолжать протекать только через тиристор VS2. Длительность интервала коммутации характеризуется обычно углом коммутации у, который может быть определен из следующего уравнения [10]: PlU Id=--- [cos a-cos (а 4- у)].(2.91) xs Обозначив угол коммутации у при углеос = 0 через у0, можно записать l-cosyo = /dxs/v/2c72.(2.92) Подставляя в исходное уравнение значение уо, получаем y = arccos [cos a+cos уо— 1] — a.(2.93) Согласно (2.93) с ростом угла а уменьшается угол коммутации у. Физическая сущность этого явления состоит в том, что с увеличением угла а растет напряжение, под действием которого развивается ток it в контуре коммутации и, следовательно, до значения Id он нарастает быстрее. Следует отметить, что длительность протекания тока в тиристорах по сравнению с идеализированной схемой увеличивается на угол у и становится равной тс+у. Процесс коммутации оказывает непосредственное влияние на выпрямленное напряжение Ud, так как на интервалах коммутации мгновенное значение выпрямленного напряжения в указанной схеме снижается до нуля (см. рис. 2.25). В результате этого происходит уменьшение среднего значения выпрямленного напряжения на AUX = тс <х + у 1 y2/y2sin9J9.(2.94) Из (2.92) — (2.94) можно получить &Ux = Idxs/n.(2.95) Среднее значение выпрямленного напряжения с учетом (2.95) равно Ud= t/docosa — IdXs/jt., ,(2.96) 2.3.2. ВНЕШНИЕ ХАРАКТЕРИСТИКИ ВЫПРЯМИТЕЛЕЙ Внешней характеристикой выпрямителя называется зависимость выпрямленного напряжения от среднего значения тока нагрузки, т.е. Ud-f(Id)- Внешняя характеристика определяется внутренним сопротивлением выпрямителя, которое приводит к снижению выпрямленного напряжения с ростом нагрузки. Снижение напряжения обусловлено активным сопротивлением схемы AUr, падением напряжения в тиристорах AUvs и индуктивным сопротивлением AUX, которое проявляется при процессах коммутации. Соответственно внешнюю характеристику выпрямителя (при roLd=oo) можно записать в виде следующего уравнения: * Ud=UdoCosa-AUr-AUvs-AUX.(2.97) Согласно (2.97) выходное напряжение выпрямителя снижается по-мере увеличения тока нагрузки Id за счет внутреннего падения напряжения. В зависимости от мощности выпрямителя влияние активных и реактивных элементов схемы в этом процессе различно. Обычно в маломощных выпрямителях преобладает влияние активного сопротивления обмоток трансформатора, а в мощных.4-индуктивного сопротивления рассеяния трансформатора. Следует отметить, что при значениях тока нагрузки, не превышающих номинальное, внутреннее падение напряжения выпрямителей, как правило, составляет не более 15—20% напряжения Udo. Однако при перегрузках и режимах, близких к короткому замыканию, становится существенным влияние внутренних сопротивлений схемы. Кроме того, в трехфазных и многофазных схемах при перегрузках изменяется характер электромагнитных процессов, влияющих на ход внешней харак- 0 ... 9 10 11 12 13 14 15 ... 49 |












