Раздел: Документация
0 ... 34 35 36 37 38 39 40 ... 365 Квадратная матрица т* размера семь является трехдиагональной. Заполняя эту матрицу, можно использовать то обстоятельство, что G является суммой диагональной матрицы и двух матриц с шестью ненулевыми элементами над и под главной диагональю. » G = 2*еуе{7) + diag(ones(l, 6), X) + diag(ones(l, 6), -1) » save G.txt G -ascii Посмотрите содержание полученных файлов (они должны находиться в подкаталоге work основного каталога MATLAB). Матрицы больших размеров удобно представлять в наглядном виде. В программе MATLAB это можно проделать при помощи визуализации матриц. В следующем разделе разобраны простейшие способы визуализации матричных данных. Визуализация матриц Матрицы с достаточно большим количеством нулей называются разреженными. Часто необходимо знать, где расположены ненулевые элементы, т. е. получить так называемый шаблон матрицы. Для этого в MATLAB служит функция spy. Посмотрим шаблон матрицы G, определенной в предыдущем разделе » G = 2*еуе{7) + diag(ones(l, 6), X) + diag(ones(1, 6), -1) После выполнения команды spy на экране появляется графическое окно Figure 1. На рис. 2.10 изображена часть окна без заголовка, меню и панели инструментов. На вертикальной и горизонтальной осях отложены номера строк и столбцов. Ненулевые элементы обозначены маркерами, внизу графического окна указано число ненулевых элементов (nz = 19). Наглядную информацию о соотношении величин элементов матрицы дает функция imagesc, которая интерпретирует матрицу как прямоугольное изображение. Каждый элемент матрицы представляется в виде квадратика, цвет которого соответствует величине элемента. Для того чтобы узнать соответствие цвета и величины элемента, следует использовать команду coiorbar, выводящую рядом с изображением матрицы шкалу цвета. Наконец, для печати на монохромном принтере удобно получить изображение в оттенках серого цвета, используя команду colormap (gray). Мы будем работать с матрицей М, определенной в предыдущем разделе. 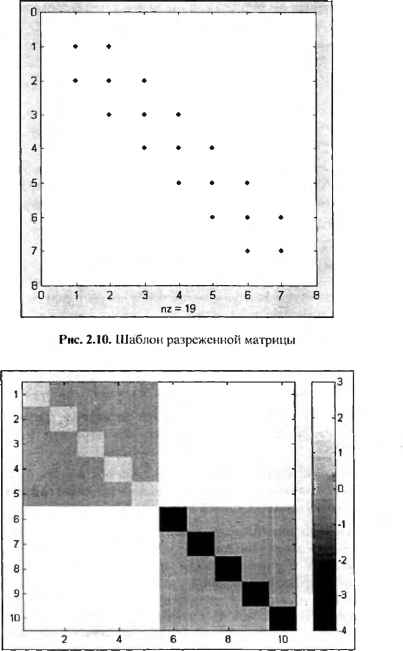 Рис. 2.11. Интерпретация матрицы как изображения Набирайте команды, указанные ниже, и следите за состоянием графического окна: » imagesc(M) » colorbar » colormap(gray) В результате получается наглядное представление матрицы, приведенное на рис. 2.11. Подробно про использование графики в MATLAB написано в следующих главах, однако уже сейчас вы можете визуализировать матрицы, с которыми мы будем работать при изучении поэлементных матричных операций. Поэлементные операции и встроенные функции Поскольку векторы и матрицы хранятся в двумерных массивах, то применение математических функций к матрицам и поэлементные операции производятся так же, как для векторов. Работа со встроенными функциями (такими как min, max, sum и т. д.) имеет свои особенности в применении к матрицам. Поэлементные операции с матрицами Введите две матрицы 25 -Г 34 9 Г-1 2 7 -3 8 -5 Умножение каждого элемента одной матрицы на соответствующий элемент другой производится при помощи оператора , * » С = А.*В С = -2 10 -8 21 -12 -45 Для деления элементов первой матрицы на соответствующие элементы второй используется . /, а для деления элементов второй матрицы на соответствующие элементы первой служит . \ » R1 = А./В R1 = -2.0000 2.5000 -0.1250 0 ... 34 35 36 37 38 39 40 ... 365
|
