Раздел: Документация
0 ... 76 77 78 79 80 81 82 ... 365 Решению вычислительных задач посвящена глава 6. Мы рассмотрим сейчас только один простой пример того, как использование файл-функций упрощает визуализацию математических функций. Только что вы построили график при помощи plot. Заметьте, что для вычисления вектора у не обязательно было вызывать myfun — можно сразу записать выражение для него и потом указать пару х и у в plot. Имеющаяся в нашем распоряжении файл-функция myfun позволяет обратиться к специальной функции fplot, которой требуется указать имя нашей файл-функции (в апострофах) или указатель на нее (с оператором е перед именем функции) и границы отрезка для построения графика (в векторе из двух элементов) » fplot<myfun, [0 4]) или » fplot(@myfun, [0 4]) Постройте графики plot и fpiot на одних осях (используйте hold on) так, как показано на рис. 5.6. График, построенный fplot, более точно отражает поведение функции, т. к. алгоритм fi ] t автоматически подбирает шаг аргумента, уменьшая его на участках быстрого изменения исследуемой функции. 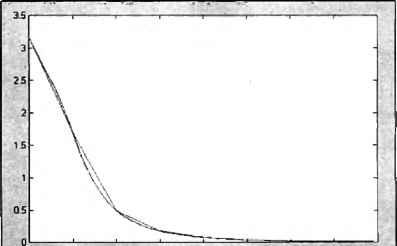 О 05t1.52 253 35А Рис. 5.6. Сравнение plot и fplot Как было отмечено в главе J, существенную роль играет выбор шага, причем неудачный выбор шага может привести к неверному результату. Вернитесь к примеру из главы 3, в котором при помощи plot требовалось построить график функции /(.v)-e"x (sin,\+ 0.1sin(lUL)7Lv)) на отрезке [0,1] и предлагалось выбрать шаг 0.01. Запрограммируйте соответствующую файл-функцию myfuni (листинг 5.4) п сохраните ее в файле myfun I .m. ;-----------...............---------............................................................................................................................................., [ Гистинг 5.4. Файл-функции для вычисления исследуемой функции function z = myfuni(t) z = exp(-t).*(sin(t) + 0.1*sin(100*pi*t)); Примечание В этом примере мы намеренно использовали z и t. Имена аргументов файл-функции могут быть любые, они никак не связаны с теми переменными, от которых будет вызываться файл-функция или в которые будет записываться результат. Например, при вызове а = myfuni (Ь) входной аргумент t станет равным ь, затем вычислится z, и переменная а примет ее значение, 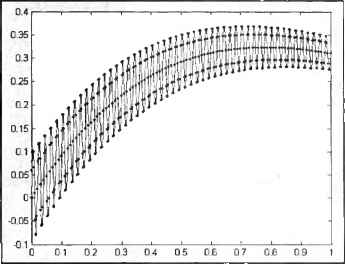 Рис. 5.7. Выбор inai а функцией f plot Для построения графика осталось вызвать fplot. Вы можете узнать о выборе значений аргумента функцией fplot, указав третьим ее входным аргументом свойства линии и маркера так же, как и в plot. Возьмите точку в качестве маркера и сплошную линию » fplot{gmyfunl, [0 1], •.-) Получается график, приведенный на рис. 5.7. Абсциссы маркеров соответствуют адаптивно подобранным значениям независимой переменной, в которых fplot вычислила исследуемую функцию для корректной визуализации. Функция fplot позволяет задавать ряд параметров, управляющих выбором значений абсцисс (см. разд. "Более подробно о fplot"главы 6). Файл-функции с несколькими входными аргументами Написание файл-функций с несколькими входными аргументами практически не отличается от случая одного аргумента. Все входные аргументы размещаются в списке через запятую. Например, листинг 5.5 содержит файл-функцию, вычисляющую длину радиус-вектора точки трехмерного про- function г = radius3(х, у. z) г = sqrt(x."2 + у.Л2 + z.*2); Для вычисления длины радиус-вектора теперь можно использовать функцию radius3, например: » R = radius3(l, 1, 1) R = Кроме функций с несколькими аргументами, MATLAB позволяет создавать функции, возвращающие несколько значений, т. е. имеющих несколько выходных аргументов. Файл-функции с несколькими выходными аргументами Файл-функции с несколькими выходными аргументами удобны при вычислении функций, возвращающих несколько значений (в математике они называются вектор-функщш). Выходные аргументы добавляются через запя- 1Л32 0 ... 76 77 78 79 80 81 82 ... 365
|
