Раздел: Документация
0 ... 94 95 96 97 98 99 100 ... 365 приближаются ступенчатой функцией, а само приближение называется интерполяцией по соседним точкам. Линейная интерполяция основана на соединении соседних точек отрезками прямых — табличные данные приближаются ломаной линией (сплайн первого порядка дефекта единица). Для получения более гладкой функции следует применять интерполяцию кубическими сплайнами. Все эти способы реализованы в функции interpi, для использования которой следует задать координаты абсцисс промежуточных точек, в которых вычисляются значения интерполянта, и способ интерполирования: □ nearest — приближение по соседним элементам; □linear — линейная интерполяция (применяется по умолчанию, если способ интерполирования не задан); □spline —интерполяция кубическими сплайнами; □1 pchip — интерполяция кубическими эрмитовыми сплайнами. При использовании pchip вторая производная сплайна может быть разрывна (в этом случае говорят, что сплайн имеет дефект два) в отличие от spline. Однако кубический эрмитовый сплайн сохраняет участки монотонности исходных данных. Выходным аргументом interpi является вектор значений интерполянта в промежуточных точках. Текст файл-программы interpidem для сравнения различных способов интерполирования приведен в листинге 6.11. ; Листинг 6.11. Файл-программа interpidem I........................................................................... ппмш. % заполнение массивов для табличной функции у. = [0.1 0.2 0.4 0.5 0.6 0.8 1.2]; у = [-3.5 -4.8 -2.1 0.2 0.9 2.3 3.7]; 11 вывод графика табличной функции маркерами plot(x, у, "ко") % задание промежуточных точек для интерполирования xi = [x(l):0.01:x(length(x))b % вычисление ступенчатой функции в промежуточных точках ynear = interpi(х, у, xi, nearest); % вычисление кусочно-линейной функции в промежуточных точках yline = interpl(x, у, xi, linear); % можно не указывать linear I вычисление кубического сплайна в промежуточных точках ysplme = interpi (х, у, xi, spline); hold on I построение графиков интерполянтов plot(xi, ynear, к, xi, yline, k:, xi, yspline, k-.) title{"Различные спбсобы интерполяции функций) xlabel(Utx) ylabel(\ity) legend(табличная функция", по соседним элементам (nearest), ... линейная (linear), кубические сплайны (spline),4) Выполнение interpidem приводит к появлению графика, изображенного на рис. 6.5, который наглядно демонстрирует способы интерполяции. Добавьте самостоятельно график кубического эрмитова сплайна, указав pchip в качестве четвертого аргумента функции interpl. Различные способы интерполяции функций 5-,--1-,-.-- э 2 1 D •1 •2 э -4 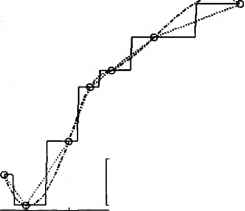 О табличная функция -по соседним элементам (nearest) ......линейная (linear) ----кубические сплайны (spline) D 0.2 0.4 0.6 0.В х 1 1.2 Рис. 6.5. Различные способы аппроксимации функций (interpl) MATLAB позволяет интерполировать не только одномерные, но также двумерные и многомерные данные. Интерполяция двумерных и многомерных данных Интерполяция двумерных данных связана с построением функции двух переменных, приближающей заданные в точках (лг,-, у,) значения г,- - Для ин- терполирования двумерных данных следует задать промежуточные узлы командой meshgrid и воспользоваться interp2, которая реализует один из способов интерполирования, в зависимости от значения последнего аргумента: □nearest — интерполяция по соседним элементам; □bilinear или linear1 — билинейная интерполяция (применяется по умолчанию, если способ интерполирования не задан); □bicubic или cubic—интерполяция бикубическими сплайнами; □* spline— интерполяция кубическими сплайнами. Примечание Для ускорения вычислений в случае равноотстоящих точек с монотонно изменяющимися координатами, соответствующих табличным данным, используются, соответственно, аргументы *nearest, *linear, *cubic или *spline\ Сравнение первых трех вышеперечисленных способов интерполяции может быть осуществлено при помощи файл-программы interp2dem, текст которой приведен в листинге 6.12. Для избежания утомительного ввода таблицы двумерных данных они генерируются при помощи некоторой функции двух переменных. I Листинг 6.12. Файл-программа interp2dem % генерирование значений табличной функции [X, Y] = meshgrid.O:0.2:1); Z = sin(3*pi*X).*sin(3*pi*Y).*ехр(-Х."2 - Y.~2); % визуализация табличной функции subplot [2, 2, 1] surf(X, Y, Z) t i tle(табличная функция) % создание сетки для промежуточных значений [Xi, Yi] = meshgrid(0:0.02:1); % интерполяция по соседним значениям ZiHear = interp2(X, Y, Z, Xi, Yi, nearest); % билинейная интерполяция (можно не указывать bilinear) ZiBiLin = interp2(X, Y, Z, Xi, Yi, bilinear); % бикубическая интерполяция ZiBiCub = interp2(X, Y, Z, Xi, Yi, bicubic); 0 ... 94 95 96 97 98 99 100 ... 365 |












