Раздел: Документация
0 ... 28 29 30 31 32 33 34 ... 78 определяется некоторым методом разбиения. Принцип, лежащий в его основе, заключается в том, что большие матрицы могут быть обработаны с помощью дополнительной памяти в каждом процессоре или путем зацикливания данных через систолическую структуру. Важной задачей при этом является минимизация времени задержки между прогонами данных или ее исключение. Для несистолических структур такая задача может быть решена путем хранения большой части матрицы внутри структуры; эта идея для задачи LU-разложения ленточных матриц полностью разработана в [16J. Здесь возникают два вопроса: какой формат данных является лучшим для разбиения и как данные должны размещаться на диске? Необходимо заметить, что эти размещения могут быть модифицированы с помощью специальных фильтров (см. гл. 22). Обычные методы разбиения логически вытекают из строчно-столбпо-вой структуры матриц. Разбиения по диагоналям и на непрямоугольные блоки присущи нетрадиционным методам, которые и необходимы для систолических структур. Основная идея здесь заключается в образовании длинных и узких матриц из коротких и широких. Так как систолические вычислители являются конвейерными, то их работа тем эффективнее, чем длиннее и устойчивее входной поток данных. Наиболее естественно метод разбиения можно представить в виде "окна" над матрицей. Окно представляет собой матрицу, над которой выполняется некоторое преобразование, и необходимый результат получается сканированием окна по исходной матрице. Дело будем иметь с большими и малыми окнами, причем малое окно будет находиться внутри большого. Аналогичными являются понятия вычислительного окна как части матрицы, находящейся в систолической структуре в течение данного времени [16, 17], и волнового фронта как переднего края окна. Представление матриц может иногда изменяться с целью увеличения производительности систолических вычислений с многократным прогоном данных через систолическую структуру. Рассмотрим два примера, в которых используются аддитивное разбиение и тензорное представление. Объем памяти в матричном процессоре часто выбирается компромиссно в зависимости от числа процессоров, и поэтому допускается некоторая вариация объема памяти данных. В общем случае меньшее число процессоров означает большее число прогонов данных, а больший объем памяти упрощает обработку матрицы большого размера. Менее изящный, но тем не менее полезный прием заключается в "удвоении" объема вычислений за счет использования времени простоя процессорных элементов в некоторых систолических структурах. Концепция аппаратной библиотеки, в которой функциональные элементы по отношению к управляющему компьютеру играют роль подпрограмм в библиотеке программ, уже обсуждалась [10]. Использование систолических структур как внешних процессоров, присоединенных к управляющей ЭВМ через разнообразные контроллеры, хорошо согласуется с этой моделью. Покажем также, что систолические структуры могут эффективно выполнять роль встроенных функциональных блоков для простых матричных 190 операций. Методы разбиения, обсуждаемые в этой главе, облегчат программирование систолических структур и проектирование полной системы их поддержки. 11.2. АДДИТИВНОЕ РАЗБИЕНИЕ Аддитивные разбиения матриц вида A = A] +А2 осуществляются в основном в устройствах матричного умножения. Их целью может быть уменьшение ширины ленты матрицы, увеличение плотности ненулевых элементов внутри ленты или уменьшение объема вычислительных ресурсов за счет использования свойств симметрии. Возможно, простейшим примером уменьшения ширины ленты матрицы является запись симметрической матрицы как M = L + LT, где L - нижняя треугольная матрица, для вычисления: хтМх = 2x?Lx. В [22] рассмотрена проблема уменьшения ширины ленты матрицы для использования в линейной систолической структуре при вычислении матрично-векторных произведений [19]. Обобщим этот метод. Диагонали матрицы А размера пХп пронумеруем от -и + 1 до и -1. Так, элемент матрицыа- лежит в / - /-й диагонали. Ширина ленты матрицы А равна w, если существуют такие целые г их, для которых выполняется неравенство -к+Kr <.v < <и - 1, так что djj =0, если/ -i<r или/ - i>s,ww=s - г +1. Таким образом, все ненулевые элементы расположены на w диагоналях матрицы А. Например, для строго нижней треугольной матрицы г =- и + 1, s -1, а для трехдиагональноТ! матрицы г = - 1, s = 1. Для любой матрицы А и целого значения w> 1 можно записать к А = Z А,-, где ширина матрицы Aj- не превышает iv. Тогда результат умножения матрицы на вектор у : = Ах может быть получен следующим образом: у := 0 for /:= 1 to do у ~ у + /4,Х с использованием линейной систолической структуры Кунга- Лейзерсона (Kung-Leiserson) для тела цикла. Здесь окно выбирает х и диагональную ленту матрицы А и движется определенным образом в зависимости от строения матрицы А. Если w =1, то данный метод называется диагональным умножением матриц [21]. Метод частичной трансляции строк (PRT) [22] осуществляется в случае, если А - заполненная матрица, w=n, к = 2, кх - верхняя треугольная часть матрицы А, А2 - строго нижняя треугольная часть матрицы А. Метод частичной трансляции столбцов (РСТ) [23] определяется аналогично, но А] - строго нижняя, а А2 - верхняя треугольные матрицы. Для очень малых значений величины w возможно использование линейно связанного массива с передачей данных от процессора к процессору, который может увеличить пропускную способность в 2 раза [13]. Матрицы А и вектор х должны быть выравнены по краям во избежание вычисления нуле- 191 вых результатов, а время между прогонами может быть сокращено чередованием верхних и нижних треугольных матриц (см. [22, рис. 4 и 5]). Метод аддитивного разбиения может быть распространен на произведение матриц <-=l 7=1 где ширина ленты как для А;, так и для Ву- не больше некоторых определенных целых чисел. В [13] рассмотрен вариант умножения заполненных матриц для к =1 - Ъ с помощью (иХи)-умножителя с гексагональными связями, где основной задачей было улучшение эффективности использования процессора, а также уменьшение ширины ленты. Другой вариант рассмотрен в [22]: путем добавления одного ПЭ к линейной систолической структуре и соответственного зацикливания данных с помощью PRT-метода можно реализовать итерации Гаусса-Зейделя или SOR. Аналогично РСТ-метод может быть применен для вычисления произведения Azx с помощью соответствующего зацикливания данных [23]. Рассмотренные методы служат для уменьшения ширины ленты, когда систолическая структура содержит небольшое число процессорных элементов (ПЭ). Скорость вычислений уменьшается с уменьшением числа ПЭ от w до w, возможно, с дополнительными потерями из-за наличия простаивающих ПЭ в одном или двух прогонах. В некоторых случаях, однако, может быть выгоднее увеличивать плотность заполнения ленты матрицы, чем скорость. Общим подходом является манипулирование со сжатым представлением матрицы, а не с исходной матрицей. Например, при решении некоторых эллиптических дифференциальных уравнений в частных производных разностными методами можно записать матрицу А в следующем виде: А = 1®В + С®1, где матрицы В и С имеют малую ширину ленты (обычно трехдиагональные) и представляют вторые разности; символ ® обозначает к ронекерово произведение. Если В и С - трехдиагональные матрицы размера иХи, то матрица А имеет размер п2Хп2 с шириной ленты 2и+ 1, но является сильно разреженной и имеет только пять ненулевых диагоналей: с номерами - п, -1, О, 1, п. Приближенное решение дифференциального уравнения может быть представлено либо как и2-вектор, либо как матрица Uразмером пХп. Тогда вектор Аи может быть представлен в виде матрицы BU + UC. Произведение An может быть получено так, как было показано: при наличии одного ПЭ, двух входных линий за время 5п2 +0(и), за 5 прогонов, или при наличии трех ПЭ, четырех входных линий, за время 4п2-Ю(п), за 3 прогона, или при наличии пяти ПЭ и двух-четырех буферов, шести входных линий за время 2и2 +0(п), за 1 прогон. Путем соединения двух систолических структур Кунга-Лейзерсона с 192 линейной систолической структурой для матричного сложения матрицу ви+ССг можно ьычислить с помощью 14и + 7 ПЭ, 4п + 8 входных линий за время Зи + 4. Естественно, матрица может быть разложена на диагонали, строки или столбцы, если это необходимо для уменьшения числа ПЭ. Основная идея заключается в том, чтобы путем изменения представления данных можно было перейти от эффективной ширины ленты, равной 5, к любой ширине ленты от 1 до 2п + 1 за счет адаптации данных к имеющемуся устройству. Огфеделенный интерес представляет работа [1] по распространению "красно-черного" упорядочения для итеративного решения линейных систем на параллельных компьютерах. 11.3. ОК-РАЗЛОЖЕНИЕ Рассмотрим теперь ортогональное приведение матрицы к треугольному виду с помощью вращений Гивенса. Базовой операцией в этом случае являются формирование линейной комбинации двух строк матрицы и замена обеих из них в матрице. Вращение является идеальным для систолического выполнения, так как более чем одна новая операция может быть применена к одной и той же паре строк столько раз, сколько данные распространяются в правильной последовательности. Если каждый процессорный элемент содержит локальную память, способную хранить один столбец матрицы, то в этом случае целесообразнее использовать триангуляцию Хаусхолде-ра; для ленточных матриц требования к объему памяти не является препятствием [ 1 /]. Систолические структуры, реализующие вращения Гивенса, делятся на три группы: с фиксированным вращением и изменяемыми элементами (матрица Q хранится в структуре); изменяемыми вращениями и фиксированными элементами (матрица R хранится в структуре) и с изменяемыми вращениями и изменяемыми элементами. Методы декомпозиции для структур Хеллера-Ипсена (Heller, Ipscn) третьей группы 111, 12] в дальнейшем будут обсуждены более подробно. Структуры второй группы описаны в работах [8, 4], причем в этих структурах используется поточная арифметика для повышения производительности процессоров. В гл. 22 даются полный анализ методов декомпозиции на основе трапецеидальных систолических (р Xq)-структур (усеченный (q Xq)-треугольник Джентлмена-Кунга) и следующая схема: 1)разбиение А= (А, А2 . . .), где А( имеет размер пХр ; А,- имеет размер nX(q-p),2<i; 2)приведение Ai к виду (у), где R -Q, А, - верхняя треугольная матрица размера р Хр; 3)зацикливание вращений и получение QiA,-, 2<i; 4)пропуск первых р строк и столбцов полученной матрицы А и повтор. Этот метод является стандартным и будет в дальнейшем использован. В первой группе методов процессорный элемент осуществляет поворот, при котором для каждой пары (х, у) и управляющего сигнала выходной результа! равен ((х2 +у2)Ч2, 0) и запоминает значение угла. По получении новой пары (дг, у) вновь осуществляется поворот и результат передается дальше. Существенным фактором является то, что для сохранения целостности алгоритма входные данные организованы построчно на каждый порт. Существует два основных способа проектирования. В первом осуществляется обнуление элементов матрицы в порядке снизу вверх [7, 3], во втором - сверху вниз [2]. Время вычисления в обоих случаях одинаково и составляет п + 2р -1 шагов для приведения матрицы размера р Хп к верхней трапецеидальной форме при использовании треугольной фхр) -структуры, содержащей р (р~ +1)/2 процессорных элементов. Метод исключения, приведенный в [7], для заполнения матриц требует кроме треугольного массива размера рХр еще половину треугольного массива ПЭ (\/2р)X (у/2р) (р (р +1)/2 процессорных элементов) и сеть полной тасовки. Увеличенный массив ПЭ представляет собой просто половину (2р)X (2р)-треугольника. Пусть А - матрица размера пХт, п<т, разбитая на блоки следующим образом: А/ А= А2 где А; - матрица размера рХт. В первых к - Гп/р 1 прогонах через (рХр)-треугольцик матрица Aj- приводится к верхней трапецеидальной форме, в результате чего край матрицы приобретает остроконечный вид. В следующих прогонах размер окна увеличивается до 2р строк и производятся вычисления: for/ = 2 to к by 1 for/ =к to / by -1 тасовка строк l А,- приведение результата к верхней трапецеидальной форме с использованием увеличенного массива за время (т - (j - 2)р) + р + I замена строк в А Так, наконец, матрица А приводится к треугольной форме за время 0{к2т + + к3р). Если п=т, то это время составит 0(п3/р2). Окно размера (2р)Хт движется снизу вверх (управляемое параметром i) внутри большего окна, которое движется сверху вниз (управляемое параметром/ ). Рассмотрим методы разбиения для QR-разложения ленточных матриц с помощью систолической структуры Хеллера-Ипсена [11, 12], которая состоит из q w ортогонально соединенных процессорных элементов в виде линейных сетей шириной q w (рис. 11.1 без треугольников). Каждая линейная сеть может обнулять одну поддиагональ диагональной iv-матрицы. Допустим, что матрица А имеет ширину ленты w и содержит р наддиагоналей и q поддиагоналей (w = p + q + 1) и что q <р. В [11, 12] предполагается, что структура характеризуется параметрами w = vv, q=q~, что позволяет привести матрицу А к верхней треугольной матри- ряс. 11.1. Дополненная систолическая матрица Хеллера-Ипсена: w=q = 3 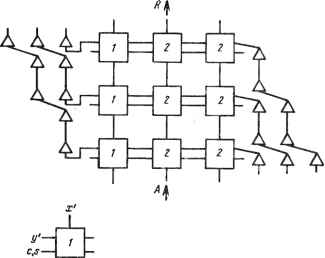 -X -CS Навходе-х, у На выходе-х=(хг+у2)/гу у=о, с=х/хг s=у/у т На входе-x,y,c,s На выходе-х= сх +sy, y=-sx* су,с, s це R за один прогон с помощью вращений Гивенса. Порядок обнуления в данном случае - сверху вниз в столбцах, как в устройствах с фиксированным вращением [3, 7]. Крайний левый ПЭ начинает поворот, и остальные ПЭ передают этот поворот дальше. В систолическую структуру на каждом шаге вводится одна побочная диагональ, начиная с верхнего левого угла матрицы. Каждый входной и выходной порты получают иливыцаютэлемен-ты одной и той же диагонали на чередующихся шагах. При w = w, q =q время получения матрицы R из А равно 2(n+q - 1), ширина ленты матрицы R всегда равна ширине ленты матрицы А. Если w <w при любых q и q, то входные данные можно дополнить w-w нулевыми наддиагоналями и пропустить матрицу через систолическую структуру Vq\q 1 раз, очищая структуру перед каждым прогоном данных. На каждом прогоне обнуляется q поддиагоналей и вращения распространяются поперек строк без зацикливания; в результате получаются q наддиагоналей. Время разложения равно Fqfq l(2n+2q -2 + t0), где г0 - время очистки систолической структуры между прогонами. Дополнительные надциагонали могут быть исключены из окончательного результата, так как они принимают нулевые значения. Может возникнуть ситуация, когда на последнем прогоне будут обнулены все поддиагональные элементы до того, как матрица выйдет из структуры (например, если q не делится на q нацело). Тогда главная диагональ подается на крайний левый процессор некоторого 0 ... 28 29 30 31 32 33 34 ... 78 |












