Раздел: Документация
0 ... 71 72 73 74 75 76 77 ... 166 Результат построения твердотельной модели для примера 4 приведен на рис. 198.  Рис. 198. Результат построения сечения строительного перекрытия Пример 5. Изгиб пружины с шагом витка 0,006 м под действием силы тяжести Последовательность действий Первым этапом построения балочной модели пружины будет создание двух вспомогательных окружностей основания пружины. Для создания окружностей нужно получить две ключевые точки - центры окружностей. Шаг 1. Создание двух вспомогательных ключевых точек Создаем две ключевые точки 1 с координатами (0; 0; 0) и 2 с координатами (0; 0; 0.03). См. пример 1, шаг 1. Шаг 2. Создание окружности Строим окружность с центром в начале координат (первая ключевая точка) радиусом 0 .003. См. пример 4, шаг 5. Замечание! Окружность должна делиться на 4 сектора. При этом нужно указать, что угловая мера дуги равно 360°. Шаг 3. Включение нумерации ключевых точек Включаем нумерацию ключевых точек. Последовательность действий аналогична рассмотренной в примере 3 на шаге 3. Шаг 4. Копирование окружности Самым простым способом создания второй окружности является копирование созданной на предыдущем шаге окружности со смещением по OZ на DZ = 0.03 т. (рис. 199). См. последовательность действий в примере 3 на шаге 12.
Рис. 199. Результат создания двух вспомогательных окружностей Замечание! После выполнения команд или пунктов меню, соответствующих шагам 1-3 текущего примера, удобно посмотреть результаты построений в изометрии (кнопка iso) меню Pan-Zoom-Rotate (Utility Menu > PlotCtrl > Pan, Zoom, Rotate) Шаг 5. Рисование вспомогательных прямых линий Попарно соединяем прямыми линиями противолежащие ключевые точки 3 и 7, 4 и 8, 5 и 9, б и 10 (рис. 200), принадлежащие окружностям. См. последовательность действий в примере 3 на шаге 2. 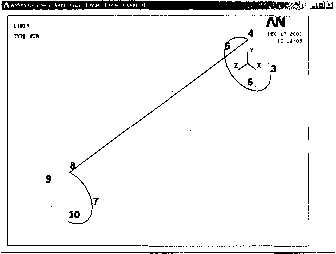 Рис. 200. Результат создания вспомогательных линий для пружины Шаг 6. Деление построенных прямых линий Делим прямую линию, соединяющую точки 3 и 7, на 5 отрезков. Остальные построенные прямые линии разбиваем на 20 равных отрезков. См. последовательность действий в примере 4, шаг 2. Шаг 7. Переход в глобальную цилиндрическую систему координат Пружина представляет собой спираль, поэтому наиболее удобно создавать линии подобной формы с использованием не декартовой, а цилиндрической системы координат (рис. 201). Переходим в глобальную цилиндрическую систему координат. Для этого используем последовательно два пункта меню: Utelity Menu > WorkPlane > Change Display Cs to > Global Cylindrical а затем Utelity Menu > Plot > Replot 0 ... 71 72 73 74 75 76 77 ... 166 |












