    
Вы находитесь в разделе Типовых решений систем безопасности
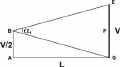
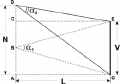
Зоны обзора видеокамер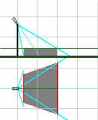 Вот только один аспект этой программы. Скажите, как обычно Вы представляете зону обзора видеокамеры? В виде треугольника, не так ли? А ведь это бывает лишь тогда, когда видеокамера находится на одном уровне с объектом наблюдения (как например, в видеопереговорных устройствах, в видеоглазках). А начнете поднимать видеокамеру - и проекция зоны наблюдения из треугольника сначала превращается в трапецию, а затем и в прямоугольник (рис. 1, 2 и 3 получены с помощью программы VideoCAD). "Ну, - скажете Вы, - это настолько редко...". Так ли? Выйдите из метро "Горьковская" в Санкт-Петербурге, перейдите через Кронверкский проспект, потом через Каменноостровский проспект (осторожно, здесь нет перехода!) и пройдите через ажурные ворота во двор дома №3. А теперь надо задрать голову как можно выше, чтобы увидеть наверху видеокамеру, которая смотрит прямо вниз, контролируя обстановку во дворе. Представьте, какая зона наблюдения у этой видеокамеры. 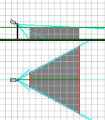  Конечно, эта программа относится только к охранному телевидению, конечно, она понадобится лишь специалистам, заинтересованным в грамотном проектировании объектов (а не тем, кто готов повсеместно, "не заморачиваясь" использовать вариообъективы). И все-таки, это серьезный шаг вперед в проектировании охранного телевидения, и я думаю, за ним последуют и другие. Наверное, не будет преувеличением сказать, что появление на российском, а теперь уже и на международном рынке, программы Станислава Уточкина Хочу пояснить, что я не собираюсь искать изъяны в этой программе, более того - мои публикации будут посвящены не столько самой программе, сколько мыслям, которые появлялись во время ее тестирования. Однако при этом хотелось бы определить те границы, где удобно и достаточно использовать простейшие калькуляторы углов обзора, а где примение программы "VideoCAD" дает неоспоримые преимущесва. Короче, зовите меня каким угодно Сальери, но я должен-таки поверить алгеброй эту программу. Так вот, историческая заслуга С.Уточкина в том, что он поднял проектирование видеосистем на качественно новый уровень, что для расчетов он использовал третью координату - высоту установки видеокамеры. Как известно, угол обзора видеокамеры по вертикали меньше угла обзора по горизонтали, что определяется соотношением сторон ПЗС-матрицы 4 : 3. С другой стороны, у меня, как и у многих специалистов возникают вопросы в отношении программы "VideoCAD". Поэтому я и решил ее тестировать, а о полученных результатах докладывать коллегам в этой рассылке и на "Мосту". Более того, я приглашаю всех заинтересованных лиц присоединиться к обсуждению данной программы на Форуме. Отсюда угол обзора по вертикали: α1 = 2 arctg (V/2L) ( Ясно, что для повышения точности расчетов можно до бесконечности учитывать различные параметры (например, что Земля - не плоская, потом, что Земля не шар и т.д.). Давайте, оценим, для начала, насколько существенно влияет на точность определения углов обзора высота установки видеокамеры. Угол обзора по вертикали  Если видеокамера устанавливается выше центра плоскости наблюдения, то необходимый угол обзора по вертикали будет уменьшаться от значения α1 до значения α2 (рис. . Это соответствует случаю, когда, например, видеокамера, контролирующая высокие музейные двери или межцеховые ворота, располагается под потолком (приблизительно на уровне верха дверей). Угол обзора в этом случае равен: α2 = arctg (EG/CE) = arctg (V/L) ( 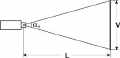 Рассчитывается этот угол из очевидного соотношения (рис. : α1 / 2 = arctg (V/2L) ( а ошибка в случае определении угла обзора по вертикали стандартным методом равна δ= * 100% / 2 arctg (V/2L) ( С одной стороны, это может быть, и не очень страшно, что при увеличении высоты установки видеокамеры возрастает зона обзора по вертикали - на экране видеомонитора будут видны не только сами двери, но и часть территории перед ними. Однако площадь отображения дверей на экране уменьшится, и хоть это лучше, чем если бы они "обрезались", но все же лучше заранее знать, как оно будет при установке видеокамеры на объекте и сознательно выбирать оптимальный вариант. Значения углов α1 и α2, а также ошибка δ представлены в табл. 1 и на графике рис.
где N - высоты установки видеокамеры, а L - расстояние до объекта наблюдения. Из треугольника ADG можно получить следующее соотношение: α2= < GDE = < CDE - < ADG ( Подставляя выражения ( и ( в ( , получаем: < CDE = 90° - < CED = 90° - arctg (CD/CE) = 90° - arctg ( Абсолютное уменьшение угла обзора по вертикали составляет < ADG = 90° - < AGD = 90° - arctg (AD/AG) = 90° - arctg (N/L) ( а ошибка определения угла по вертикали в случае использования стандартного метода ( равна α2 = 90° - arctg - 90° - arctg (N/L) = arctg (N /L) - arctg ( Из последнего выражения нетрудно заметить, что при N = V выражение (1 преобразуется в ранее рассмотренное выражение ( , а выражение ( - в выражение (1 . Δ= α1 - α2 = 2 arctg (V/2L) - arctg (N/L) - arctg (1 Это следует учитывать, когда, например, требуется контролировать автомобили перед шлагбаумом у въезда на парковку с тем, чтобы в поле зрения видеокамеры максимальным образом попадали государственные регистрационные знаки и лица водителей. Для задачи автоматического опознавания автомобильных номеров их достоверное определение возможно, если наклон видеокамеры к поверхности дороги составляет угол, не превышающий 30°, что определяется соотношением N/L. Мертвая зона под видеокамерой δ= 2 arctg (V/2L) - arctg (N/L) - arctg * 100% / 2 arctg (V/2L) (1 Чтобы определить длину мертвой зоны m следует рассмотреть треугольник ADG, в котором необходимо опустить перпендикуляр PQ на основание AG.  В соответствии с этими формулами были рассчитана относительная погрешность определения угла по вертикали δ для углов 10°, 20° и 30° в зависимости от отношения N/L и построены соответствующие графики (рис. . Из этих графиков следует, что чем меньше расстояние до объекта наблюдения и чем выше устанавливается видеокамера, тем реальный угол обзора по вертикали будет меньше по сравнению с рассчитанным по формуле ( . Из подобных треугольников ADG и QPG следует: 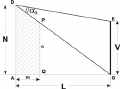 Весьма важным вопросом при проектировании системы охранного телевидения является учет мертвой зоны под видеокамерой. откуда: Перпендикуляр PQ длиной n может служить в качестве примера высоты человека (естественно, если мы оцениваем длину мертвой зоны AQ на предмет обнаружения человека). Иначе говоря, окажись человек высотой n правее точки Q, он попадет на экран видеомонитора (для простоты рассуждений overscan не учитываем). Окончательно для длины мертвой зоны получаем: AD / PQ = AG / QG (1 , Из выражения (1 следует, что если высота человека n стремится к 0 (злоумышленник ползет), то длина мертвой зоны максимальна и составляет m = L (расстояние до объекта наблюдения). Наоборот, если высота установки видеокамеры N равна высоте человека n, то человек сразу же попадает в поле зрения видеокамеры (m = . Характерно, что угол обзора по вертикали в явном виде не входит в выражение (1 . AQ = AG – QG = AG – PQ*AG / AD = AG*(AD – PQ) / AD (1 . m = L*(3 – 1, / 3 = 0,4 L (1 m = L*(N – n) / N (1 . Продолжение следует Чтобы оценить промежуточные значения длины мертвой зоны, следует задаться высотой человека. В качестве примера для конкретности примем, что n = 1,8 м. В этом случае, если, например, видеокамера установлена на высоте 3 м, то длина мертвой зоны равна: Иначе говоря, при расстоянии до объекта L = 5 м длина мертвой зоны составляет n = 2 м, при L = 15 м длина мертвой зоны n = 6 м. Как видим, полученные значения достаточно значительны, чтобы их игнорировать. Более того, их следует учитывать при выборе параметров других видеокамер.
Читайте далее:  Эротика в дизайне-2, или обзор тенденций в дизайне проксимити считывателей Скудные возможности Система контроля доступа как надежный элемент системы безопасности Безопасный спуск Скуд и ip не надо строить баррикады Проксимити считыватели мирового качества по российской цене 5.3. активные компоненты Управляя временем Новая версия системы контроля доступа компании keri systems Как создать систему безопасности, которая работает с новыми технологиями Десять лет спустя Я помню, как все начиналось ,часть 3, Я помню, как все начиналось ,часть 6, Я помню, как все начиналось ,часть 9, 11 - 17 сентября 2006 года |
