Раздел: Документация
0 ... 7 8 9 10 11 12 13 ... 34 Равенство (3.73) позволяет по частным коэффициентам чувствительности Хуу и Хух определить полные коэффициенты чувствительности Аух с учетом как непосредственного, так и косвенного влияния относительного приращения 8х на величину 5у. Частные коэффициенты чувствительности Хуу и Хух определяются дифференцированием функций (3.65). Если функции (3.65) не могут быть выражены в явном виде, их дифференцирование может быть проведено, как дифференцирование неявных функций. Некоторые коэффициенты X могут быть даже найдены опытным путем, если нет удовлетворительного математического выражения, связывающего величины yt и у1 или у- и х,: Разделение параметров на зависимые у} и независимые х, является условным, так как при усложнении задачи независимая переменная х, может стать зависимой. Так, окружающая температура, рассматриваемая как независимая переменная, при учете тепловыделения светильника уже не является независимой. Расширение задачи (включение в рассмотрение дополнительных переменных) приводит к увеличению размеров матрицы \Хуу\. [Ч] - ~Х(1) -УУ ЛУУ х% , (3.74) При нахождении обратной матрицы [Ч] ~1 для определения полных коэффициентов чувствительности удобно использовать обратные матрицы [ЧТ и [X.J,2/], т. е. использовать определенные ранее коэффициенты чувствительности для более ограниченных задач. Матрицыи [Х.] являются матрицами связи и в большинстве практических задач заполнены слабо [3.12]. При слабом заполнении этих матриц удобно пользоваться направленными графами матрицы. На рис. 3.16 показан направленный граф относительных приращений параметров для линейного индуктивного ПРА без потерь. При рассмотрении индуктивно-емкостного ПРА с потерями граф индуктивного ПРА может быть использован в качестве подграфа (рис. 3.17). По рассмотренным общим выражениям нами получены конкретные выражения для коэффициентов чувствительности всех основных схем ПРА. По графу, приведенному на рис. 3.16, найдены коэффициенты чувствительности для линейного индуктивного ПРА без потерь: арл и3 = (Ч/л + р Ч"л) Ч и, I А> ДрЧЧ/.+рЧОЧь,/ Лл Сл,« = (Ч Сл + Чл Ч Р. ) / Д; Аидр1* = ЧдрРлРЧь./А (3.75) Рис. 3.16. Направленный граф относительных приращений параметров линейного индуктивного ПРА без потерь где Рис. 3.17. Направленный граф относительных приращений параметров индуктивно-емкостного ПРА с потерями (Л—подграф линейного индуктивного ПРА) Д=1 + р-1,18/иэ/(1-1,18/иэ).(3.76) На рис. 3.16: 5LK — относительное изменение коэффициента самоиндукции за счет изменения конструктивных параметров; 5 £/л к — относительное изменение напряжения на лампе U„ за счет конструктивных факторов. Значение 5 £/л „ измеряется при номинальном токе лампы. Для линейного индуктивно-емкостного ПРА с потерями вычисление коэффициентов чувствительности проведено по графу (рис. 3.17): * лЭ Л а ! А1л£л,Ч,и„ p..l. (3.77) где ApLj и Л/л(/э вычислены для схем индуктивного ПРА без потерь; А — определитель графа: Д= 1 -А(;л(;ээ»э +Ч»э~Ч1эЧл;(ЗЛ8) Р*Гпь,—коэффициент передачи прямого пути от узла 8LK к узлу 5.РЛ; Apti — алгебраическое дополнение пути PrLj, ХллКч=л..-(1-Ч«,Ч,+л-Ч«Лл)+л«чЧ.Ч«Р-79) I Остальные полные коэффициенты чувствительности вычисляются аналогично. Из векторной диаграммы (рис. 3.10) получены выражения для частных коэффициентов чувствительности: (coscp3 + f/JS)t/JS 1 + Ut cos(p3 > « l + U%cos<p3 (p3t/Jsin q>3 "Л l + C/Jcosq), (3.80) где Ui=I3R/U3. При использовании-нелинейного дросселя необходимо учитывать действующую индуктивность дросселя L в соответствии с (3.50). Однако действующая индуктивность L зависит от напряжения на дросселе £/др (рис. 3.18). Поэтому возникает добавочная зависимость Ьш„= -Ня„КНя„-аВяНяе1Вя-1),(3.81) где ст—приведенная величина воздушного зазора, определенная по (3.48), гя„ /Я. 55. (3.82) которая определяется по характеристике намагничивания стали. Теперь коэффициенты чувствительности для нелинейного дросселя Лн могут быть выражены через коэффициенты чувствительности для схемы с линейным дросселем Лл. Для коэффициентов, не затрагивающих узлы 5L и 5 Uap, Лн =ЛЛ + Для коэффициентов, связывающих 5£/др и (или) 5L, Л" Д» =-у—- ~ (3.83) (3.84) "ДР" ""др Коэффициенты чувствительности получили широкое применение при анализе различных параметров ПРА. 3.5. АНАЛИЗ АНОМАЛЬНЫХ РЕЖИМОВ В ЦЕПЯХ С РАЗРЯДНЫМИ ЛАМПАМИ Лампа по различным причинам может работать в так называемых аномальных режимах, параметры которых сущест- 62 Рис. 3.18. Направленный граф относительных приращений параметров нелинейного индуктивного ПРА (Я—подграф линейного индуктивного ПРА с потерями) венно отличаются от нормального режима. Например, в ртутных лампах низкого давления при дезактивации одного из катодов существенно возрастает напряжение перезажигания разряда в тот полупериод горения, когда катодом служит дезактивированный электрод. Ртутная лампа высокого давления при разрушении защитной колбы лампы может не разгореться, и тогда напряжение на ней составляет всего 20—40 В вместо обычных 110—140 В. При зажигании ламп с помощью зажигающего устройства при неисправных лампе, зажигающем устройстве или ПРА (стабилизирующем элементе) пусковой режим может затянуться на длительное время, что, как правило, приводит к превышению температуры ПРА. Нормативные документы на ПРА (ГОСТ 16809-78, Публикация № 82 МЭК и др.) предусматривают сохранение ограниченной работоспособности аппаратов в аномальных режимах. Согласно документам нормируется допустимое превышение температуры элементов ПРА в самом тяжелом из возможных для конкретного ПРА аномальном режиме. В настоящем параграфе сделаны анализ аномальных режимов, возникающих в цепях с разрядными лампами, и сравнение их с пусковым режимом, который, как правило, хорошо исследован для большинства ПРА. Выделим для анализа три режима. 1.Пусковой режим стартерной схемы. В этом режиме лампа замкнута накоротко контактами стартера, т. е. можно пользоваться полученными ранее выражениями при £/л = 0 (m, = тп = 0). 2.Режим разгорания лампы высокого давления. В этом режиме форма напряжения на лампе остается приблизительно трапецеидальной, но из-за малого значения напряжения U„ коэффициент тэ = 0,1н-0,2. Схемы можно рассчитывать по выражениям, полученным ранее. 3.Аномальный, несимметричный, режим имеет место при увеличении напряжения перезажигания в один полупериод до Uz = = 700 -f- 900 В. Такой режим существенно отличается от всех режимов, рассмотренных ранее, и характеризуется существенной паузой тока. Анализу этого режима посвящен настоящий параграф. 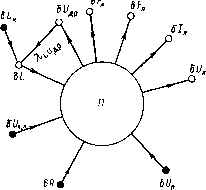 При анализе аномальных режимов возникает ряд особенностей. Во-первых, расчет первого приближения методом эквивалентных синусоид, как правило, дает большую погрешность, а ряд эффектов вообще не может быть обнаружен. Так, анализ индуктивно-емкостного ПРА при работе лампы в аномальном несимметричном режиме может привести к неверному результату (/л = 0). Этим, по-видимому, объясняется тот факт, что такой режим многие годы не принимался во внимание и ПРА часто выходили из строя в течение первого года эксплуатации. Во-вторых, расчет аномальных режимов может проводиться со значительно меньшей точностью, так как поставленная задача — оценить электрические перегрузки, возникающие в этих режимах, допускает погрешность 10—15%. В-третьих, в многоламповых ПРА вероятность работы в аномальном режиме двух или более ламп исчезающе мала и поэтому аномальный режим может рассчитываться только при одной неисправной лампе. С учетом сказанного для расчета аномальных режимов принимаем следующий метод: в качестве первого приближения рассчитываем линейную схему с постоянными параметрами R, L и С. Определяем все электрические режимы цепи; учет нелинейности ведем заменой постоянных параметров R, L и С на эквивалентные, рассчитанные с учетом нелинейных характеристик элементов и прежде всего дросселя. Уточняем электрические режимы цепи и проводим расчет при новых значениях параметров нелинейных элементов; учитывая оценочный характер расчетов, пренебрегаем теми параметрами, влияние которых незначительно. Так, расчеты сложных цепей ведем с использованием прямоугольной аппроксимации напряжения на лампе (5 = 0) и, как правило, не учитываем потери мощности в конденсаторах и другие.  Рис. 3.19. Форма напряжения на лампе «л (0) и потокосцепления дросселя Ч* (0) при работе лампы с индуктивным ПРА в режиме односторонней проводимости 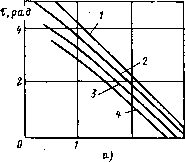
2 (р,рад 0 2 f,pu.d Рис. 3.20, Зависимость длительности горения т от начальной фазы <р при работе лампы в режиме односторонней проводимости: о — индуктивный ПРА без потерь [Л/(со/,) = 0]; б—с потерями [R/(toL) = 0,2]; при UJU„ равном: /—0; 2—0,2; 3—0,4; 4—0,6 С помощью этого метода были проанализированы схемы следующих ПРА: стартерных индуктивных, индуктивно-емкостных и бесстартерных с индуктивно-емкостным балластом и накальным трансформатором [3.13]. Приведем некоторые результаты этого анализа. Индуктивный балласт. Расчетная схема стартерного ПРА с индуктивным балластом показана на рис. 3.7. Уравнение контура у/2 Un sin (0 + ф) == со d4/d9+Мл + ил (0). Решение проводилось при несимметричном напряжении перезажигания: С/г1 = (1, 2, 3) ил и Uz2>y/2Un. Временные зависимости мл(0) и *Р(0) для этих условий приведены на рис. 3.19. Как видно, в таком режиме лампа проводит ток в одном направлении. Если напряжение перезажигания U22<>j2UB, то через лампу будет протекать ток и во вторую половину периода. Однако такие несимметричные режимы являются менее опасными, и в дальнейшем во внимание приниматься не будут. Расчет режима односторонней проводимости проведен для двух значений потерь в дросселе: i?/(coL) = 0 и i?/(coL) = 0,2. Из рис. 3.19 видно, что длительность горения лампы в течение одного периода питающего напряжения т>л. Проведенные работы показали, что длительность горения т зависит от угла перезажигания ф, который может быть найден из равенства sinФ =Un).(3.85) Зависимость т от ф показана на рис. 3.20. Видно, что учет активного сопротивления дросселя R лишь незначительно (на 0 ... 7 8 9 10 11 12 13 ... 34 |












