Раздел: Документация
0 ... 5 6 7 8 9 10 11 ... 34 Таблица 3.1. Основные соотношения для контура ламна—идеальный индуктивный балласт
При использовании коэффициентов А, В и С, рассчитанных для реальной кривой намагничивания электротехнической стали, коэффициент самоиндукции дросселя L0 на линейном участке при постоянном сечении S магнитопровода равен L° = /(<T+l/uHa4)(3-4?) где /—средняя длина силовой линии; цнач — магнитная проницаемость стали на линейном начальном участке [для холоднокатаной стали р„ач = 6,8-10~3 Тл ДА см), для горячекатаной стали Цнач = 5 • 10~3 Тл/(А -см)]; а — относительный воздушный зазор. 48 Таблица 3.2. Основные соотношения для контура ламна—нелинейный индуктивный балласт
В соответствии с [3.5] о = /в/(/сТ + /в)-0,798-10б/7в,. (3.48) где /в и /ст — соответственно длина воздушного зазора и средняя длина пути магнитных силовых линий в магнитопроводе (стали); ув — коэффициент, учитывающий рассеяние и выпучивание магнитного потока в зазоре (ув= 1,05 ч-1,2). Коэффициент нелинейности дросселя с воздушным зазором к = к0/(1+\1иача).(3.49) Для холоднокатаной электротехнической стали &0 = 2,94, для горячекатаной ко = 0,94. Рис. 3.7. Расчетная схема индуктивного ПРА 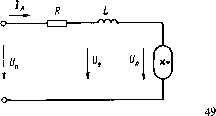 т3=0,30 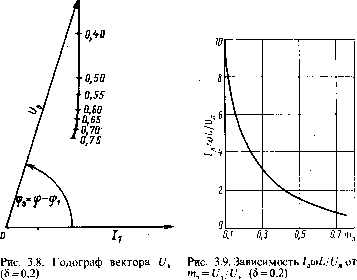 Математические выражения, приведенные в табл. 3.1 и 3.2, позволяют легко найти первое приближение при расчете конкретных схем ПРА. На рис. 3.7 представлена расчетная схема реального индуктивного ПРА. Здесь резистор R учитывает потери в дросселе. Учет потерь последовательным сопротивлением является приближенным, но при уровне потерь в стали магнитопровода Рст/Рл0,2 дополнительная погрешность расчета при таком способе учета потерь не превышает 1%. Расчет первого приближения для указанной схемы удобно вести с применением годографа вектора 1/э (рис. 3.8) и вспомогательного графика, приведенного на рис. 3.9. Зависимости построены по формулам, приведенным в табл. 3.1 и 3.2, и справедливы как для линейного, так и для нелинейного дросселя. Для нелинейного дросселя учитывается эквивалентная индуктивность дросселя [3.5]: J(l+kK,0D\)2 + (kK,0D[f где Ка0 — коэффициент амплитуды тока в схеме с линейным дросселем, Ка0-1лтах/ 7JI = ,imex/(/]IL0). С помощью годографа вектора U3 расчет первого приближения удобно вести по векторным диаграммам (рис. 3.10). На 50 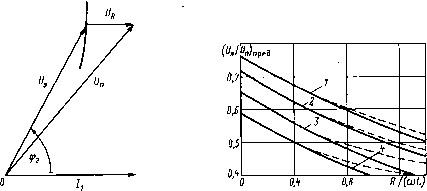 Рис. 3.10. Векторная диаграмма индуктивного ПРА Рис. 3.11. Условия работы без пауз тока для индуктивного ПРА: -—первое приближение; ----точное решение: / — UIUn=\,0; 2—1,25; 3—1,5; 4—1,75 рис. 3.11 представлены предельные зависимости, при которых осуществляется режим без пауз тока. На рисунке показано первое приближение, рассчитанное по векторным диаграммам, и точное решение, полученное на ЭВМ с учетом 3, 5 и 7-й гармоник. Как видно, первое приближение удовлетворительно описывает процесс при Л/(со/,)<0,5, что выполняется в подавляющем большинстве индуктивных ПРА. Для повышения точности расчетов все вычисления по векторным диаграммам целесообразно вести аналитически с использованием формул, приведенных в табл. 3.1 и 3.2. Такие расчеты сравнительно нетрудоемки при применении простейших калькуляторов. 3.3. АНАЛИЗ ИНДУКТИВНО-ЕМКОСТНОГО БАЛЛАСТА В соответствии с изложенным в § 1.3 для расчета индуктивно-емкостного ПРА с разрядной лампой целесообразно использовать метод гармонического анализа и синтеза. Ниже приведен расчет указанного контура при работе с исправной лампой. Из анализа аномального режима, рассматриваемого в § 3.5, следует, что этот режим представляет определенную опасность для индуктивно-емкостного ПРА и накладывает довольно жесткие ограничения на линейность ВАХ индуктивного элемента. Поэтому расчет проводится лишь для линейного индуктивно-емкостного ПРА без потерь [1.24]. Последнее обстоятельство связано с тем, что пренебрежение потерями и использование зависимости прямоугольной формы, аппроксимирующей напряжение на лампе, дают примерно одинаковые по абсолютному значению и противоположные по знаку систематические по- In с L "э % 0 1,0
0,2 ff,* 0,5 0,8 тп Рис. 3.12. Расчетная схема иидуктивно-емкостного ПРА Рис. 3.13. Кратность тока короткого замыкания для линейного индуктивно-емкостного балласта без потерь при й2 ранном: /—1,5; 2—2,0; 3—2,62; 4—3,0; 5—3,5 грешности расчета основных электрических параметров контура. Уравнение электрического состояния для рассматриваемого случая (рис. 3.12) при синусоидальном напряжении питания ип = у/2 £7nsin(9— ф) имеет вид хс J /л(в)л+<//л(8)/л=и11(е)-ил(е). (3.51) Здесь угол ф учитывает сдвиг фазы питающего напряжения относительно нуля тока лампы при Q2 = (co0/co)2 = 1/(со LC)>1. При прямоугольной симметричной аппроксимирующей форме с амплитудой, равной действующему значению напряжения на лампе С/л, мгновенное значение этого напряжения согласно (1.3) и 1Ь\ = Ъ. X ""(2,7-1)8 (3.52) Тогда wL(n2-l) /2со8(8-ф)- 4ге„(П2-1) у cos(2g-l)8 (3.53) Подставляя в (3.53) сумму функционального ряда в свернутом виде в интервале 0<9<л для Q#2g-1, получим Таблица 3.3. Суммы числовых рядов для различных значений П Функция fx й fM АЩ Сумма числового ряда при П, равном
wL(n2-l) 2 cos (9-ф)- -™"<n2-1> fsinQ9-tgcosQ9 Q \6 2 (3.54) Используя граничное условие /=0 при 9 = 0, находим фазу напряжения питания относительно начала, отсчета: к (3.55) где fQ)-- я(П2-1)4 кО.~ ,~ . ——- tg — и при£2 # 2q — 1 является суммой 00 П2-1 числового ряда вида £ д2 —Значения/Х(Щ приведены в табл. 3.3. Действующее значение токав контуре можно найти, применяя одно из следующих соотношений для /л: ;(9)</9 1/2 либо /„ I п 4=1 1/2 Первое соотношение предпочтительнее применять при отсутствии пауз тока в контуре, т. е. тогда, когда можно воспользоваться свойством ортогональности гармонических составляющих при интегрировании. Второе соотношение используется при наличии пауз тока. С учетом ортогональности, а также (3.53), получим 1/2 4 = Ail+3n /2(П)-2Л(П) (3.56) где /к — ток при закороченной разрядной лампе (ток короткого замыкания) 0 ... 5 6 7 8 9 10 11 ... 34 |












