Раздел: Документация
0 ... 3 4 5 6 7 8 9 ... 34 и общее выражение для тока лампы ~ t g0exp iMuJdt Lo l+MKI/o-l) (2.14) При периодическом переменном напряжении на лампе с периодом Ти установившийся режим наступает при условии т„ MuJdtO.(2.15) В силу нелинейности функции Мi (ил) и среднее, и действующее напряжения на лампе зависят от его формы. Так, при синусоидальной форме ил = (0 среднее и даже действующее значения напряжения на лампе меньше, чем при прямоугольной форме напряжения. Этим частично объясняется некоторое снижение напряжения на лампе на повышенной частоте. И, наконец, в-третьих, в импульсных режимах при экспоненциальном нарастании и снижении напряжения и тока во всем диапазоне изменения постоянной времени фронта импульса (от 0,2 до 100 мкс) наблюдается качественное и количественное совпадение рассчитанной и экспериментальной формы импульсов напряжения и тока. Погрешность расчетов амплитуды импульсов перенапряжения не превосходит ±8%, скорости изменения тока лампы +6%. Таким образом, рассмотренная математическая модель ВАХ люминесцентных ламп адекватна в широком диапазоне частот и при различных режимах работы ламп. Высокочастотная граница применимости модели, по-видимому, должна быть связана с тепловой инерцией теплоемкости электронного газа. Однако даже при фронте нарастания и спада импульсов напряжения и тока около 0,2 мкс не обнаружено возникновения заметных инерционных процессов. Для ламп типа ДРЛ наилучшие результаты дает математическая модель, приведенная в [2.9, 2.10]: dgjdt=gl М, {u,) = F, (ил; gj;(2.16а) dldt=M2(uJ(fiy„- = F2(ua; Р);(2.166) Сл = Р#л = 4/"л,(2.16в) где Руст — установившееся значение Р при ил = const. Как видно из (2.16), модель лампы типа ДРЛ состоит из двух нелинейных дифференциальных уравнений первой степени (2.16а) -и (2.166) и алгебраического уравнения (2.16в). Введение второго дифференциального уравнения связано с тем фактом, что в лампах типа ДРЛ при сравнительно более высоком 36 Таблица 2.6. Значения коэффициента Ал для ламп ДРЛ различных мощностей
в [2.9] (2.17) (2.18) давлении паров ртути необходимо учитывать инерционность изменения электронной температуры. Для аппроксимации нелинейных коэффициентов предложены выражения 0,4 + 0,6(И/£/0) М2(ил)=\0+[1,5 + 3(\ил\1иоу-5]; руст = 0,4 + 0,6«л/£/0. Значения постоянного коэффициента Ал для ламп типа ДРЛ разной мощности приведены в табл. 2.6 [2.10]. Погрешности расчета при анализе режимов электромагнитных ПРА с лампами ДРЛ при отсутствии паузы тока лампы не превышают +3%. В режимах с паузами тока и в импульсных режимах с различными балластами погрешности не превосходят ±7%. К сожалению, до настоящего времени не разработаны математические модели ламп типов ДНаТ и ДРИ. Использование для расчета режимов с этими типами ламп моделей (2.16) приводит к значительной погрешности, которая в ряде сложных режимов может достигать 30—35%. Глава третья РАСЧЕТ СХЕМ ПРА С ИСПОЛЬЗОВАНИЕМ ПРИНЦИПА ШТРАУХА 3.1. ОБЩИЕ ВОПРОСЫ РАСЧЕТА ЦЕПЕЙ ПРА Как уже отмечалось выше, принцип Штрауха применим, когда форма напряжения иМ) может быть принята в некоторых пределах независимой от формы тока лампы 4(f). Поэтому методы, основанные на этом принципе, применимы в основном 37 для расчетов традиционных электромагнитных схем включения. Однако и ряд схем с полупроводниковыми стабилизирующими устройствами может быть проанализирован указанными методами. В настоящей главе на основе принципа Штрауха и методов припасовывания и гармонического анализа проведен анализ основных типов ПРА при работе с исправной лампой и с лампой, один из электродов которой дезактивирован. В отдельный раздел выделены методы расчета коэффициентов чувствительности, учитывающие изменение режима работы лампы при малых изменениях параметров схемы, напряжения источника питания и т. д. Все расчеты проведены с использованием математических моделей, описанных в гл. 2. Для анализа электрических цепей ПРА, работающих на промышленной частоте, разработаны дополнительные расчетные методы [3.1, 3.2]: метод переменных коэффициентов, общие условия работы лампы без пауз тока и ряд других, которые изложены ниже. Преобразование характеристик нелинейных двухполюсников. При анализе электрических цепей переменного тока с нелинейными безынерционными двухполюсниками (например, нелинейными дросселями и конденсаторами, трансформаторами, диодами и т. д.) в зависимости от характера рассматриваемого вопроса используются различные типы характеристик: мгновенных, средних или действующих значений, одной или нескольких гармонических составляющих. Обычно необходимая характеристика рассчитывается по соответствующей характеристике для мгновенных значений. Однако такие пересчеты характеристик весьма трудоемки и их нужно проводить заново при всех изменениях характеристик нелинейных элементов. Рассмотрим метод переменных коэффициентов, который позволяет существенно облегчить пересчет характеристик нелинейных двухполюсников, особенно при некоторых вариациях его характеристик. В ряде случаев метод позволяет по характеристикам действующих и средних значений электрических параметров и спектральному составу сигналов восстановить нелинейную амплитудную характеристику или характеристику для мгновенных значений электрических величин. В методе переменных коэффициентов характеристика нелинейного элемента представляется в виде [3.2] y = a[x + kf(x)],(3.1) где х, у — мгновенные значения электрических величин, связанные характеристикой нелинейного элемента; к— коэффициент 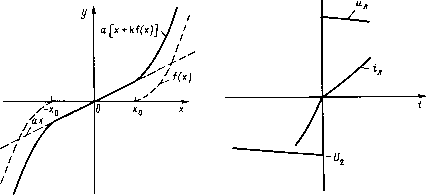 Рис. 3.1. Аппроксимация характерис- Рис. 3.2. Форма напряжения на лампе тики нелинейного элементаил (t) и тока лампы /л (t) при пере- зажигании лампы (режим без пауз тока лампы) нелинейности характеристики; f(x) — произвольная нелинейная функция. При к = 0 нелинейная характеристика переходит в линейную, у=ах. Мерой нелинейности характеристики может служить модуль \к\. Нелинейная функция f(x) может иметь весьма произвольный вид. Например, на рис. 3.1 показана характеристика нелинейного элемента, у которого функция f(x) симметрична и имеет излом в точке х0: = 0, если хх0; >0, если х>х0. В качестве нелинейной может выбираться и несимметричная функция, неоднозначная для нелинейных характеристик с гистерезисом, и даже функция с конечным числом разрывов второго рода. В соответствии с методом переменных коэффициентов действующее значение j(9) при x(Q) с периодом Тп выражается соотношением Y = Y0 Jl+2kA(Xm) + k2b{Xm),(3.2) где Y0 = aX—действующее значение функции j(9), найденное для линейного двухполюсника с характеристикой у = ах; А(Хт) и В(Хт)—безразмерные переменные коэффициенты, определяемые интегральными функциями Р(х; 9) вида х"[/(х)]ехр(У-2я9е/Тп)Л р(х; в)= «!---(3.3) где р, I, и=1,. 2, 3...; у = -1. Переменные коэффициенты зависят от вида функции /(*), формы д:(Э) и амплитуды Хт и не зависят от коэффициента нелинейности к. При заданной функции f(x) и постоянной форме х/Хт, например х(в) / Xm = sin 0, переменные коэффициенты зависят только от амплитуды Хт. В цепи с нелинейным элементом спектр y(Q) отличается от спектра x(Q). Для нахождения спектрального состава y(Q) можно ввести переменные коэффициенты Dq(Xm). Тогда эффективное значение косинусоидальной и синусоидальной составляющих при q=l, 2, 3... Yq=Yq0 + kYm0Dq(Xm);(3.4) Y"9=Y;0 + kYm0D"t(Xm)(3.5) и действующее значение q-й гармоники Y=y/Y*+Y?,(3.6) где Yq0, Yq0— эффективные значения косинусоидальной и синусоидальной составляющих; Ym0 = aXm—амплитуда y(Q) в цепи с линейным двухполюсником. Аналогично для среднего за период значения функции + kYm0D0(Xm).(3.7) При однозначной функции f[x) может быть найдено среднее значение модуля функции за половину периода Т„/2: YCp,мод= ср,модо [1+C(Arm)],(3-8) где коэффициенты А, В и D не являются независимыми. Связь между , ними может быть установлена из выражения для действующего значения j;(B): Y=Y0Jl+2kA(Xm)+k2b(Xm) = IY2cp+ £ Y\. (3.9) V4=1 Возведя в квадрат и приравнивая члены с одинаковыми степенями, получим A = Xm/x(xcpd0/X+ £ Xqdq/X+ £ X;d;/x); (3.10) b={Xm/X)2{D20 + D12 + D[2+ ...),(3.11) где Хср и X—соответственно среднее и действующее значения x(Q); Xq; X"q—действующие значения косинусоидальной и синусоидальной составляющих q гармоник. Равенство (3.10) учитывает спектральный состав функции и существенно упрощается при синусоидальном воздействии. Конкретные зависимости коэффициентов А, В, С, D от Хт при различных типах нелинейных характеристик будут рассмотрены ниже. Условия работы лампы без пауз тока. Рассмотрим в общем виде условия работы лампы без пауз тока при питании от источника промышленной частоты. Для простоты рассмотрим одноламповую схему, причем результаты легко могут быть распространены и на многоламповые схемы. Пусть перезажигание лампы происходит в момент времени t = 0 (рис. 3.2). В этот момент ток лампы /л = 0, и напряжение на лампе изменяется скачком от —U2 до +UZ при практически постоянном напряжении питания. Отсутствие паузы тока характеризуется положительной производной din / dt>0 во время перезажигания. Напряжение на лампе ил(г) препятствует протеканию тока, поэтому после перезажигания скорость нарастания тока лампы . уменьшается. Таким образом, в момент перезажигания происходит изменение производной тока лампы так, что dia (- 0) / dt > din (+ 0) / dt > 0.(3.12) Переход к работе с паузами тока происходит при Лл( + 0)/Ж = 0.(3.13) Необходимым условием работы без пауз тока является отсутствие скачков тока в момент перезажигания, вызванных изменением напряжения на лампе, так как такие скачки могут привести только к изменению знака производной din( + 0)/dt и, следовательно, к появлению паузы тока. Скачок тока будет отсутствовать при Ш(Р4Л = Ш=0,(3.14) р\р р Z{p)JZ{p) где Z(p) — операторное входное сопротивление схемы включения со стороны лампы. В общем виде оно имеет вид z(P)=fl+fl;11+-+fl-(з-15) Условие (3.14) выполняется при «>/. Разница между степенью числителя и знаменателя в (3.15) не может быть больше единицы, поэтому п = I +1 и выражение для Z(/?) может быть представлено в виде z)=a°p,+af?"+a+1-(3-16) 0 ... 3 4 5 6 7 8 9 ... 34
|
