Раздел: Документация
0 1 2 3 4 5 6 7 ... 34 зация плазмы положительного столба разряда, форма напряжения на лампе может быть весьма сложной и существенно зависит от режима работы лампы. Рассмотренные выше динамические характеристики разрядных ламп соответствуют исправной лампе при достаточной эмиссии обоих электродов. Однако к концу срока службы лампы довольно распространенным является случай, когда один из электродов лампы полностью дезактивирован. При этом возрастает напряжение перезажигания в полупериод, при котором дезактивированный электрод является катодом. Эксперименты, проведенные на люминесцентных лампах, прогоревших более 10 тыс. ч, и на специально изготовленных люминесцентных лампах с одним дезактивированным электродом, показали, что напряжение перезажигания может достигать 700—900 В, а напряжение горения практически остается неизменным [2.4]. Если при возрастании напряжения Uz схема не обеспечивает перезажигания лампы в один из полупериодов, то она начинает работать в режиме односторонней проводимости. При высоком перезажигающем напряжении лампа работает в аномальном несимметричном режиме, который может возникать, например, в индуктивно-емкостных аппаратах. Лампы высокого давления (типов ДРЛ, ДНаТ) также могут к концу срока службы переходить в аналогичные аномальные режимы. Однако эти лампы применяются, как правило, с аппаратами с невысоким перезажигающим напряжением, и из аномальных режимов, возникающих при дезактивации одного электрода, известен лишь режим односторонней проводимости. Исключение составляют лампы типа ДРИ, у которых для нормального разгорания (см. ниже) необходимо весьма высокое перезажигающее напряжение. Поэтому некоторые лампы типа ДРИ могут переходить в аномальный несимметричный режим, что необходимо учитывать при анализе их электрических режимов. 2.3. АЛГЕБРАИЧЕСКАЯ АППРОКСИМАЦИЯ ВАХ РАЗРЯДНЫХ ЛАМП При расчетах электрических цепей с разрядными лампами их реальные ВАХ заменяются более простыми аппроксимирующими выражениями. В качестве таких используют алгебраические и тригонометрические полиномы и ряды или дифференциальные уравнения. Поэтому принято все аппроксимации ВАХ разрядных ламп разделять на алгебраические и дифференциальные. Каждая из аппроксимаций имеет свои преимущества и недостатки. Рассмотрим алгебраические аппроксимации, которые широко применяются для расчета и анализа электрических цепей ПРА. Рис. 2.4. Статические характеристики люминесцентных ламп в двойном логарифмическом масштабе при диаметре лампы, мм: /- 19; 2—25; 3—38 Для аппроксимации статических ВАХ разрядных ламп (рис. 2.4) обычно используется уравнение [2.5] и„ = ВРл,(2.3) где В и р — постоянные коэффициенты [р<0 для падающих статических характеристик (характеристики с отрицательным наклоном) и р>0 для возрастающих статических характеристик]. Уравнение (2.3) удовлетворительно аппроксимирует статическую ВАХ дуги в области токов /л = (0,2-н2) 7„ом. Оно может быть преобразовано к виду UJU„ = (IJI„Y(2.4) или в дифференциальной форме {dUJdIa):(UJIa)=p.(2.5) В табл. 2.1 приведены значения р, рассчитанные для различных типов ламп по статическим характеристикам, полученным при включении ламп в сеть промышленной частоты. Электрические параметры номинальных люминесцентных ламп при включении с образцовым измерительным дросселем (ДОИ) приведены в табл. 2.2. Там же даны средние значения коэффициента рср и средние квадратические отклонения стр, рассчитанные для всей совокупности ламп. Экспериментальное исследование статических характеристик ламп типа ДРЛ показало, что в области рабочих токов при постоянной температуре горелки р= — (0,08 ч-0,12), а при установившейся равновесной температуре горелки р = 0,04 н-0,06. Для аппроксимации динамических ВАХ разрядных ламп широко используют различные алгебраические выражения, с определенной точностью аппроксимирующие зависимость ил = =/(/л) или un(t). При аппроксимации функции un(t) имеют дело с вольт-секундной аппроксимацией, которая широко применяется для расчетов схем ПРА. В [1.2] было отмечено, что при изменении вида электромагнитного балласта на промышленной частоте, коэффициента тП=ия/ U„, типа лампы основные 25 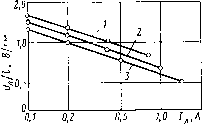 Таблица 2.1. Значения коэффициента р для различных типов ламп
изменения ил=/(/л) связаны с изменением формы тока, в то время как функция мл(г) практически не изменяется! Указанное было подверждено рядом исследований [1.5, 1.10], что позволяет в отмеченных случаях аппроксимировать лишь зависимость ил(г), т. е. заменять лампу при расчетах эквивалентным генератором (см. § 1.3). В зависимости от требуемой точности расчета применяемые аппроксимирующие выражения могут иметь различную сложность. Наиболее простая аппроксимация — аппроксимация эквивалентной синусоидой, когда лампа заменяется линейной эквивалентной схемой с параметрами R3 и Ьэ [2.3]. На промышленной частоте такая аппроксимация приводит к большой погрешности Таблица 2.2. Электрические параметры и значения коэффициента р для номинальных люминесцентных ламп по ГОСТ 6825—74 при постоянной температуре колбы лампы
(до 15—20%), однако на повышенных частотах напряжение на лампеприближается к синусоидальному и аппроксимация обеспечивает достаточную точность расчетов при синусоидальной форме напряжения источника питания [2.3]. При этом на повышенной частоте индуктивная составляющая Ьэ = 0, так как напряжение и ток лампы практически совпадают по фазе. Замена лампы эквивалентным резистором Яэ иногда используется и при несинусоидальном напряжении источника питания и даже при импульсном питании, однако погрешность расчета таких режимов возрастает. Основной недостаток аппроксимации эквивалентной синусоидой при расчете ПРА на промышленной частоте — высокая погрешность. При такой аппроксимации невозможно рассчитать искажения тока лампы, переход к режиму горения с паузами тока и ряд других параметров. Наиболее сложной из применяемых аппроксимация является четырехугольная (рис. 2.5, а [1.14]). Разложение в ряд Фурье согласно (1.3) дает Мл(9) = %н и -(2,-1)9- 2а) ,f!(2-7-1 (2-6) где а = 0,175-0,262 рад [1.14]. . Значения среднего напряжения горения лампы UTcp — = (U1 + U2)/2 и относительного спада напряжения на лампе за полупериод b = (U1 — U2)/2UT<:p были введены в аппроксима-ционные выражения А. Е. краснопольским [1.5]. Расчет с использованием (2.6) достаточно сложен, поэтому его следует применять лишь в тех случаях, когда погрешность расчета не должна превосходить 1—2% [1.10]. 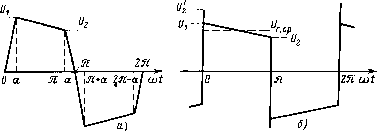 Рис. 2.5. Аппроксимация напряжения лампы при синусоидальном токе: а четырехугольная; о — трапецеидальная Из (2.6) легко получить другие аппроксимационные выражения, которые чаще всего применяют в инженерных расчетах. Полагая а = 0, раскрывая неопределенности типа 0/0 в (2.6) и заменяя ряды их суммами в свернутом виде [1.10], получим для интервала 0 9 я: Ме)=С/г,ср(1+5-259/4(2-7) Данная аппроксимация (рис. 2.5,6 [1.5]) с достаточной для инженерной практики точностью позволяет рассчитывать большой класс схем электромагнитных ПРА на промышленной частоте, причем в основном таких, в которых эквивалентное сопротивление балласта носит индуктивный характер. Для схем с емкостным балластом целесообразнее использовать прямоугольную аппроксимацию [1.12], т. е. положить в (2.6) а = 0 и 5 = 0. Таблица 2.3. Значения коэффициента 6
Рис. 2.6. Модель лампы в виде безынерционного переключателя Рис. 2.7. Возникновение паузы тока при низком перезажигающем напряжении и схеме включения лампы с резистивным ПРА Для режимов с паузами тока лампу следует рассматривать как безынерционный переключатель на три положения, управляемый напряжением и током (рис. 2.6). При горении лампы (переключатель в любом крайнем в зависимости от направления тока положении) напряжение на ней равно ur(t). Погасание лампы происходит при снижении тока до нуля (переключатель переходит в среднее положение). Перезажигание лампы происходит при напряжении Uz (переключатель переходит в другое крайнее положение). На рис. 2.7 показано возникновение паузы тока при низком перезажигающем напряжении при включении лампы с резистивным ПРА. В табл. 2.3 приведены значения коэффициента 5 для различных типов разрядных ламп. Среднее напряжение горения UT ср при 5<0,3 и работе лампы без пауз тока приблизительно равно действующему значению напряжения на лампе: Un = JlIn] Ulср(1 + 5 - 259/я Y dQ = Uucp V1 + 1 /352 * UT,ep, его значение можно взять из нормативной документации на лампы. Для исправных люминесцентных ламп и ламп типа ДРЛ при работе в режимах без пауз тока и в режимах с малой паузой можно считать, что UzzzU1 =(1,2 + 1,25) Ua. Для люминесцентных ламп с дезактивированным катодом необходимо учитывать увеличение напряжения перезажигания до 700—900 В (рис. 2.8). У металлогалогенных ламп напряжение перезажигания может быть выше, чем у ламп типа ДРЛ. Особенно это проявляется в период разгорания, когда температура горелки составляет 180—220° С, что связано с образованием при этих температурах отрицательных ионов двухиодистой ртути и быстрым спадом концентрации электронов при снижении тока 0 1 2 3 4 5 6 7 ... 34
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
