Раздел: Документация
0 ... 21 22 23 24 25 26 27 ... 34 влияние которых заметно сказывается при больших сопротивлениях шунта Лш. В [6.13] показано, что сопротивление рассеяния обмоток необходимо учитывать при мощности Рл>400 Вт. При меньших мощностях эти сопротивления на два порядка больше магнитного сопротивления шунта Ящ. На основе расчета проводимостей по зависимости /?ш=/(/в) может быть определен воздушный зазор /в. С увеличением мощности и напряжения на вторичной обмотке трансформатора воздушный зазор растет. Наличие ферромагнитного корпуса ПРА приводит к росту воздушного зазора магнитного шунта в 1,4—1,6 раза по сравнению с открытой конструкцией, что объясняется влиянием потока рассеяния в корпусе трансформатора. Метод расчета трансформатора с магнитным шунтом был распространен и на автотрансформаторы с полным или частичным включением первичной обмотки [6.14—6.17], которые целесообразно использовать в схемах включения разрядных ламп при относительно небольших кратностях превышения напряжения холостого хода над напряжением источника питания (UlxIUY 1 + 2). При этом цепь с автотрансформатором заменяется схемой с эквивалентным трансформатором и эквивалентной лампой, так что все основные соотношения, полученные для трансформатора с магнитным шунтом, становятся пригодными и для автотрансформатора. Следует отметить, что при расчете трансформатора и автотрансформаторах магнитными шунтами, так же как при расчете дросселя, могут учитываться дополнительные ограничения по применению унифицированных пластин, типовых магнитопроводов и т. д. 6.8. ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТОВ ш,, е, С ПОМОЩЬЮ ЭВМ Минимизация множителя g может быть проведена независимо от электрических параметров ПРА при сравнительно слабых ограничениях только по физической реализуемости, т. е. га, > 0, и, > 0, > 1. При минимизации методом градиента в каждой точке поиска К определяют gradg и делают «шаг» в направлении, противоположном направлению градиента. В новой точке К+1 снова определяют градиент и т. д. В каждой новой точке необходимо проверять условие убывания функции, т. е. gic+i<gK- Если это условие не выполняется, то «шаг» уменьшают и точку К+2 берут ближе к точке К на направлении gradg. Решение проводится с постоянным шагом Н0, который уменьшают каждый раз, как только функция g начинает возрастать. Эта процедура продолжается до тех пор, пока значение функции станет неизменным при уменьшении шага. Считается, что g(mK, п%, е,) является решением, если выполняется неравенство \gK+i и„ е,) — gK(mx, пх, еж)\(%, где \—заданная точность вычислений. Структурная схема программы, реализующей описанный выше процесс вычислений, приведена на рис. 6.20. На первом этапе происходит засылка исходных данных Ка, К„ X, mt0, пж0, еж0, g0 и начального шага Я0. После 144 Рис. 6.20. Структурная схема минимизации функции g и вычисления оптимальных значений /и , п , 8„ Засылка. \исхвдных данных тко,пнвекО Засылка пк0 ~*~пк,тек ек0 ~*"к, тек 90 -"Як.тек <0 дки~9к1-б Печать тк>"«ек. 9тъп >0 За.да.ни.8 к тех OffpCLLULBHULe к вычислению Анализ 9кч~9к Вычисление дд/дек >0 Вычисление тек "к*Л v£g/4)HTe„*/7K+J обращения к вычислению функции g(mK, ик, е„) проверяется условие убывания функции. Если это условие не выполняется gK+1 >gK , то шаг Н0 уменьшается и вся программа повторяется, а если выполняется, то происходит сравнение При невыполнении этого условия вычисляют частные производные, находят направление градиента и полученные координаты новой точки снова засылают в рабочие ячейки и цикл повторяют. Если условие \gK+i~fjlf; выполняется, то результаты выводятся на печать и проводится аналогичный расчет при новых значениях Ки, Kt и X. Результаты расчета приведены на рис. 6.21 —6.24. При изготовлении дросселя не всегда возможен точный выбор оптимальных значений шк, и,, е„. Поэтому на рис. 6.21 —6.24 нанесены предельные значения т,,пр, "к, пР, e«, пр, при которых изготовленный дроссель будетотличаться от оптимального на 3%, если только один параметр т„ и, или е, отличается от оптимального. На рис. 6.21 — 6.24 видно, что соотношения размеров оптимального дросселя не зависят от его полной мощности Uapi, заданных значений вш и j. Приведенные зависимости "к.опт, йк.опт. е,,опт от X позволяют рассчитать размеры оптимальных дросселей, выполненных из различных марок электротехнических сталей и других материалов с использованием медного, алюминиевого и других проводов. Рис. 6.21. Зависимости коэффициентов т„, ик, ек для дросселя с магнитопро-водом типа П2: -Е«.о, 5—е 7—л. 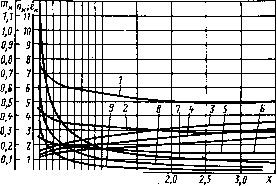 0 0 0,2 0Л ftff ДО 7,0 7,5 Рис. 6.22. Зависимости коэффициентов тк, и., е.. для дросселя с магнитопрово-дом типа Ш (спецификация по рис. 6.21) 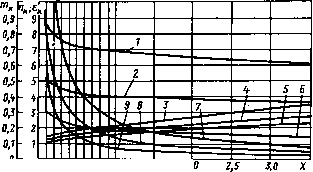 о цг м о,в о,в 7,0 1,5 г, Рис. 6.23. Зависимости коэффициентов т , и,, ек для дросселя с магнитопрово-дом типа Ш (спецификация по рис. 6.21)
 О 0? 0,4 0,6 0,8 10 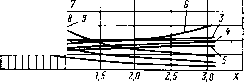 Рис. 6.24. Зависимости коэффициентов /я„ ик. дросселя (спецификация по рис. 6.21) е, для сборно-стержневого 6.9. КОНСТРУКТИВНЫЙ РАСЧЕТ ДРОССЕЛЕЙ С ПОМОЩЬЮ ЭВМ На основе конструктивного расчета дросселей, изложенного в [6.18], разработана программа ДРОСЛ, предназначенная для индуктивных, емкостных и компенсированных ПРА для разрядных ламп. Программа составлена на языке ФОРТРАН и применяется на ЭВМ «Минск-32» и серий ЕС-1022, ЕС-1033 и др. Алгоритм расчета, основанный на методе динамического программирования, позволяет определить конструктивные и экономические показатели ПРА на П-образном магните-проводе с одной и двумя катушками, на Ш-образном и сборно-стержневом магнитопроводах. Его можно использовать для расчета ПРА на ленточном магнитопроводе. Метод расчета применим к аппаратам открытого и закрытого исполнений, а также дает возможность рассчитывать балласты при использовании медного и алюминиевого обмоточного проводов, при работе на промышленной или повышенной частоте, в широком диапазоне мощностей разрядных ламп. Метод позволяет согласовать ограничения, накладываемые на различные параметру дросселя, оценить их влияние на его стоимость. Программа ДРОСЛ доведена до уровня сервисной программы, в которой наряду с исходными данными на печатающее устройство выводятся результаты расчетов, сведенные в таблицу (ширина стержня, толщина набора, ширина окна, диаметр провода, число витков, число слоев и т. д.). Одновременно на печать выводятся все экономические показатели (массы стали и провода, потери в стали и обмотке и т. д.). Программа позволяет одновременно рассчитывать 12 вариантов дросселей 147
\Аа Вычисление экономических показателей. I Печать результатов Рис. 6.25. Укрупненная структурная схема программы «ДРОСЛ» при различных исходных данных. Время расчета зависит от количества вариантов и типа машины (для ЭВМ «Минск-32» оно не превышает 3—5 мин). Укрупненная структурная схема программы ДРОСЛ показана на рис. 6.25. Блок 2 выделен в отдельную подпрограмму ОПТИМ, блоки 4 и 5 — в подпрограмму ВСТАВ. Полная структурная схема подпрограммы ОПТИМ показана на рис. 6.26. Подпрограмма обеспечивает расчет оптимальных значений Вт и J при заданных исходных параметрах и значениях коэффициентов тк, пк, ек. В программе реализуется алгоритм, основанный на сечении области допустимых Вт и J прямыми Bm = XJ (рис. 6.27). Такие сечения начинаются с начального значения Х0, и в точках пересечения 1—4 определяются значения J. Для точки, в которой значение J минимально, определяется и запоминается произведение (BmJ)0. Затем коэффициент Х0 увеличивается на АХ, (X = Х0 + АХ), и вычисляется новое значение (BmJ)v Если (BmJ)1>t[BmJ)0, то Xt увеличивается на АХ (Х2 = Х,+АХ), и процесс повторяется. Вычисления повторяются до тех пор, пока значение (BmJ)K не начнет уменьшаться: В соответствии с рис. 6.27 (BmJ)K+i<(BmJ)K. При этом от Xx + i отнимается 2АХ и расчет проводится с меньшим 148 От блока.! 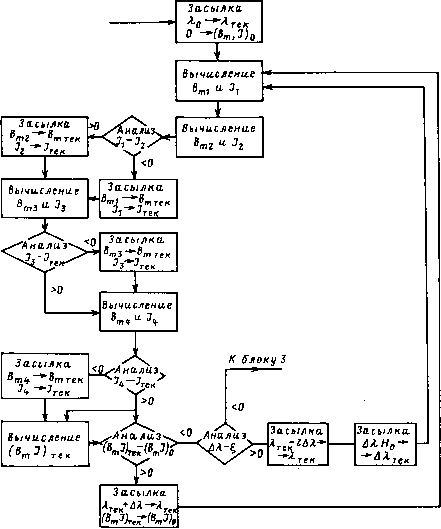 Рис. 6.26. Структурная схема подпрограммы «ОПТИМ» для расчета Вт и J шагом АХ/10. Расчет заканчивается, когда шаг АХ/10" <£. Значение % выбрано таким, что погрешность определения в самом неблагоприятном случае не превышает 0,1%. В блоке 3 проводится расчет геометрических размеров магнитопровода и катушки, числа витков и диаметра провода. Затем в блоках 4 и 5 (подпрограмма ВСТАВ) уточняется 149 0 ... 21 22 23 24 25 26 27 ... 34 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||












