Раздел: Документация
0 ... 26 27 28 29 30 31 32 ... 365 при помощи последовательности команд, приведенной ниже: » х = -1:0.005:-0.3; » f = sin{x.,-2) ; » g = sin(1.2*x."-2); » plot(x, f, x, g) 11-1-1--T—"-r--1—r 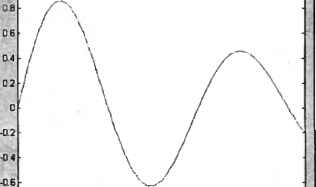 ob1.....1" ........... ............-1-1-1-1-1-1-1 0 0.1 0.2 0.3 0.4 0 6 0.6 0.7 0.8 09 I Рис. 2.4. Гладкий график функции Получившиеся графики, приведенные на рис. 2.5, дают наглядное представление о поведении исследуемых функций. MATLAB выводит графики разным цветом. Монохромный принтер напечатает графики различными оттенками серого цвета, что не всегда удобно. Команда plot позволяет легко задать стиль и цвет линий, например, » plot(x, f, k-, х, g, k:) осуществляет построение первого графика сплошной черной линией, а второго -— черной пунктирной (рис. 2.6). Аргументы к- и к: задают стиль и цвет первой и второй линий. Здесь к означает черный цвет, а дефис или двоеточие— сплошную или пунктирную линию. Визуализация данных и построение графиков подробно описаны в следующих главах. Окно с графиком можно закрыть, нажав на кнопку закрытия окна в его правом верхнем углу. 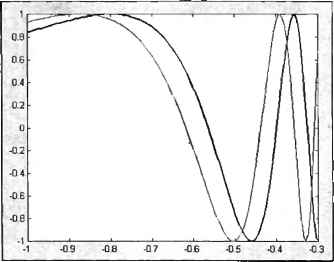 Рис. 2.5. Два графика на одних осях 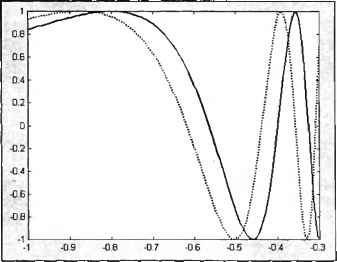 Рис. 2.6. Изменение стиля н цвета линии графиков Построение графиков функций в MATLAB гребует понимания работы с векторами — необходимо уметь вводить векторы, использовать двоеточие для автоматического заполнения с заданным шагом, применять поэлементные операции для вычисления функций от вектора значений аргумента. Все эти вопросы были разобраны выше. Две следующие главы посвящены более детальному использованию графических средств пакета. Перейдем теперь к умножению векторов. Умножение векторов Вектор можно умножить на другой вектор скалярно (это произведение еще называют внутренним), векторно, или образовать так называемое внешнее произведение. Результатом скалярного произведения является число, векторного — вектор, а внешнего — матрица. Скалярное произведение Скалярное произведение векторов а и Ъ длины N , состоящих из действительных чисел, определяется формулой N Следовательно, для вычисления скалярного произведения необходимо просуммировать компоненты вектора, полученного в результате поэлементного умножения а на b, т. е. надо использовать функцию sum и поэлементное умножение. Найдите самостоятельно скалярное произведение векторов
Ниже приведена требуемая последовательность команд: » а = [1.2; -3.2; 0.7]; » Ъ = [4.1; 6.5; -2.9]; » s - sum(a.*b) s = -17.9100 Скалярное произведение векторов можно также вычислить, применив функцию MATLAB dot » s = dot(a,b); Найдите длину (или, как еще говорят, модуль) вектора а \а\ - <Jaa . 0 ... 26 27 28 29 30 31 32 ... 365
|
