Раздел: Документация
0 ... 27 28 29 30 31 32 33 ... 365 Решение: » d = sqrt(dot(a, а)) d = 3.1886 Векторное произведение Векторное произведение a xb определено только для векторов из трехмерного пространства, т. е. состоящих из трех элементов. Результатом также является вектор из трехмерного пространства. Для вычисления векторного произведения в MATLAB служит функция cross: » а = [1.2,- -3.2; 0.7] ; » Ь = [4.1; 6.5; -2.9]; » с = cross(а, Ь) Для тренировки попробуйте вычислить axb+bxa. Если получился вектор, состоящий из нулей, то вы все проделали правильно, т. к. для любых векторов выполняется свойство axb = -bxa . Смешанное произведение векторов а, Ъ, с определяется по формуле abc-a-bxc). Модуль смешанного произведения векторов равен объему параллелепипеда, построенного на этих векторах так, как показано на рис. 2.7. с = 4.7300 6.3500 20.9200 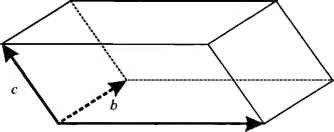 О а Рис. 2.7. Параллелепипед, образованный тремя векторами Найдите объем параллелепипеда, если
Правильные действия таковы: » а = [3.5; 0; 0]; » Ь = [0.5; 2.1; 0] ; » с = [-0.2; -1.9; 2.8]; » V = abs(dot(a, cross(b, с))) V = 20.5800 Внешнее произведение Внешним произведением векторов а = {а . b = (bk)k=i м называется матрица С = (с/А.) ( размера NxM , элементы которой вычисляются по формуле Вектор-столбец а в MATLAB представляется в виде двумерного массива размера /V на один. Вектор-столбец b при транспонировании переходит в вектор-строку размера один на М. Вектор-столбец и вектор-строка есть матрицы, у которых один из размеров равен единице. Фактически С = аЬт, где умножение происходит по правилу матричного произведения. Для вычисления матричного произведения в MATLAB используется оператор "звездочка": » а = [1; 2; 3]; » Ь = [5; 6; 7] ; >> С - а*Ь С = 5 6 7 10 12 14 15 18 21 MATLAB вывела в командное окно матрицу в привычном виде— по строкам. Используйте команду whos для просмотра переменных рабочей среды или окно Workspase. Числа, векторы и матрицы хранятся в двумерных мае- сивах числа — в массивах, размерностью один на один, вектор-столбцы и вектор-строки содержатся в массивах, у которых одно из измерений равно единице, а для матриц выделяются двумерные массивы подходящих размеров. Именно поэтому операции и встроенные функции в MATLAB приспосабливаются к виду аргументов, выдавая результат в соответствующем виде. Если вы внимательно изучили использование векторов, то читать следующие разделы о работе с матрицами не представит большого труда. Двумерные массивы, матрицы В этом разделе описан ввод матриц, математические операции с ними, поэлементные операции, вычисление функций от элементов матриц, чтение и запись с использованием текстового файла, простейшая визуализация матричных данных. Ввод матриц, простейшие операции Различные способы ввода Вводить небольшие по размеру матрицы удобно прямо из командной строки. Введите матрицу размерностью два на три (3 1 -Л А - [2 4 Ъ) Для хранения матрицы используйте двумерный массив с именем а. При вводе учтите, что матрицу А можно рассматривать как вектор-сголбец из двух элементов, каждый из которых является вектор-строкой длиной три, следовательно, строки при наборе отделяются точкой с запятой: » а = [3 1 -1; 2 4 3] а = 3 1-1 2 4 3 Для изучения простейших операций над матрицами нам понадобится еще несколько матриц. Рассмотрим другие способы ввода. Введите квадратную матрицу размера три так, как описано ниже:
0 ... 27 28 29 30 31 32 33 ... 365
|
