Раздел: Документация

0 ... 52 53 54 55 56 57 58 ... 365

Таблица 3.3 (окончание)

Что требуется	Команда ТеХ	Результат
Выделение жирным шрифтом одного символа или текста	Шаблон матрицы (\bfM)	Шаблон матрицы M
	(\bfA4X) фильтра	АЧХ фильтра
Набор символа или текста жирным курсивом	Векторы {\bf\itx) и {\bf\ity}	Векторы х и у
	{\bf\л г.Оптимальная) кривая	Оптимальная кривая
Изменение шрифта и его размера	(\fontname{arial}\fonts ize{14}г-функция}	Z-функция
Степень, верхний индекс	хл{2)	х2
	(\itxn2.5}	х2-5
	lUteJMNit-x)	е~х
Нижний индекс	f )5)	и
	f (\itxx(	fxv

Примечание

Прямой шрифт текста в ТеХ устанавливается командой \rm. Для получения обычного прямого шрифта можно не указывать никаких команд.

Возможно использование греческих букв и специальных символов, например title (Зависимость при a=\pi) приводит к заголовку: "Зависимость при а = л". В табл. 3.4 и 3.5 приведены команды ТеХ для вставки некоторых прописных и строчных греческих букв и специальных символов.

Таблица 3.4. Греческие буквы

Команда	Символ	Команда	Символ	Команда	Символ
\alpha	а	\lambda	X	\chi	X
\beta	Р	\mu	Й	\psi
\gamma	У	\nu	V	\omega	to

---

Таблица 3.4 (окончание)

Команда	Символ	Команда	Символ	Команда	Символ
\delta	5	\xi		\Gamma	Г
\epsilon	Е	\rho	p	\Delta	Д
\eta	Ч	\sigma	о	\Theta	0
\theta	9	\tau	X	\Lambda	Л
\kappa	к	\phi	ф	\Phi	Ф

Таблица 3.5. Специальные символы

Команда	Символ	Команда	Символ
\leq	<	\leftrightarrow	<->
\geq	>	\leftarrow	<—
\pm	+	\rightarrow	->
\propto	ОО	\downarrow	I
\partial	э	\uparrow	т

Текст в формате ТеХ можно использовать в качестве аргумента функций title, xlabel, ylabel при построении двумерных графиков и в тех же командах вместе с zlabel для трехмерных графиков.

В качестве упражнения создайте график, изображенный на рис. 3.38.

Ниже приведена последовательность команд, обеспечивающих требуемый результат.

» [X, Y] = meshgrid(0:0.05:1, -2:0.05:0);

» Z = -exp(-Y."2),*cos(3*pi*X>.*Х.*<1 - Х).*У;

» surfc(X, У, Z)

» colormap(gray)

» colorbar

» title (1 График (Utz) =- {\ite} * {-{\ity} Л {2} } cos(3 \pi {\itx})... (\itx) (1 - {\itx}) {\ity})

» xlabel(1x1)

» ylabel(1 у1)

» zlabel( z )

---

График 7 = - еу соеСЗ л>0* (1-х)у

o.db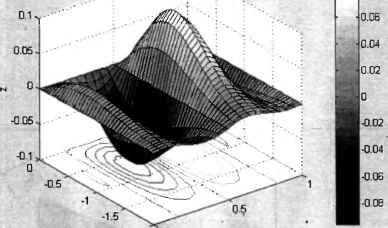

у-2 0

Рис. 3.38. Задание для самостоятельной работы

По умолчанию в MATLAB поддерживается основной формат ТеХ, однако имеется возможность перейти к расширенному формату LaTeX для набора более сложных формул. Мы вернемся к этому вопросу в главе 9, поскольку он связан с обращением к свойствам текстовых объектов, каковыми являются заголовок и подписи к осям (см. разд. "Текстовые объекты"главы 9).

Поворот графика, изменение точки обзора

Примеры, приведенные в предыдущих разделах, свидетельствуют о том, что при построении трехмерных поверхностей оси координат располагаются всегда одинаковым образом. Часть поверхности остается при этом скрытой. Для получения полной информации о поверхности ее желательно "осмотреть" со всех сторон. Положение наблюдателя за системой координат, изображенной на рис. 3.36, характеризуется двумя углами: азимутом (Az) и углом возвышения (El). Азимут отсчитывается от оси, противоположной у, а угол возвышения от плоскости ху. На рис. 3.39 положительные направления отсчета обозначены стрелками.

Изменение положения наблюдателя относительно графика в MATLAB осуществляет функция view. Аргументами view являются азимут и угол воз-

0 ... 52 53 54 55 56 57 58 ... 365