Раздел: Документация
0 ... 55 56 57 58 59 60 61 ... 365 Это можно проделать при помощи команд » [Ае, El] = view; » surfl{X, Y, Z, [Az-90, 0]) » shading interp в результате получается освещенная поверхность, изображенная на рис. 3.45. 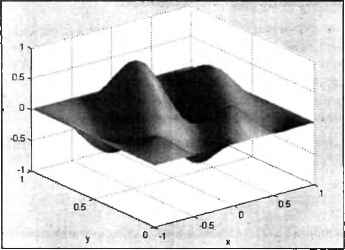 Рис. 3.44. Освещенная поверхность  о -1 Рис. 3.45. Изменение положения источника света Анимированные графики При изучении движения точки на плоскости или в трехмерном пространстве полезно не только построить траекторию точки, но и следить за движением точки по траектории. MATLAB предоставляет возможность получить ани-мированный график, на котором кружок, обозначающий точку, перемещается на плоскости или в пространстве, оставляя за собой след в виде линии — траектории движения. График похож на летящую комету с хвостом. Для построения анимированных графиков применяются функции comet и comet3. Постройте, например, траекторию движения точки в течение 10 секунд, координаты которой изменяются по закону , ч smt , ч cos/ *(0=—г ?()=- t+i Действуйте точно так же, как при построении графика параметрически заданной функции, но для визуализации результата используйте commet: » t = [0:0.001:10]; » х = sin(t)./(t+1); » у = cos(t)./(t+1); » comet{x, y) При выполнении последней команды следите за тем, чтобы окно с графиком было поверх остальных окон. Окончательный вид траектории движения приведен на рис. 3.46.  Рис. 3.46. Окончательный вид траектории движения (commet) Скоростью движения кружка можно управлять, задавая различные шаги при автоматическом заполнении вектора, соответствующего времени. Использование comet с одним аргументом (вектором) приводит к построению динамически рисующегося графика значений элементов номера в зависимости от их номеров. Функцию comet можно вызвать и с третьим дополнительным числовым параметром, который задает длину хвоста кометы. По умолчанию он равен 0.1. Обратите внимание, что при изменении размеров графического окна или при его минимизации и последующем восстановлении траектория движения пропадает. Это связано со способом, который применяет MATLAB для построения графика. Получите самостоятельно траекторию движения фиксированной точки на окружности, катящейся по прямой (циклоиду). Циклоида описывается параметрическими зависимостями л(/) = / —sin/, y(/) = l-cos/. Для построения траектории точки, перемещающейся в пространстве, используется функция comet3. Пусть координаты точки в течение 100 секунд изменялись по следующему закону -г-50/50 .-I/—501/50 л=е 1 1 sin/, у = е 1 1 cos/, z — t. Отобразите траекторию движения точки, применяя приведенные ниже команды: » t = 0:0.1:100; » х = exp(abs{t - 50)/50).*sin(t); » у = exp(abs(t - 50)/50).*cos(t); » z = t; » comet3{x, y, z) Функцию comet3 можно вызывать с четвертым числовым аргументом, который так же, как и в случае comet задает длину хвоста кометы. Работа с несколькими графиками Во всех примерах, приведенных в предыдущих разделах, графики выводились в специальное графическое окно с заголовком Figure 1. При следующем построении графика предыдущий пропадал, а новый выводился в то же самое окно. MATLAB предоставляет следующие возможности работы с несколькими 1рафикамн: □вывод каждого графика в свое окно: □вывод нескольких графиков в одно окно (на одни координатные оси); 0 ... 55 56 57 58 59 60 61 ... 365 |












