Раздел: Документация
0 ... 58 59 60 61 62 63 64 ... 365 В результате получается графическое окно, изображенное на рис. 3.50, которое содержит шесть подграфиков, наглядно демонстрирующих способы построения трехмерных графиков в MATLAB. Обратите внимание, что последняя команда coiormap(gray) изменяет палитру всего графического окна, а не подграфиков по отдельности. Визуализация векторных полей Функции compass, feather и quiver графически представляют совокупность двумерных векторов. В качестве примера построим зависимость вектора скорости u = (ux, иу} тела, брошенного под углом к горизонту, от времени: т здесь их0, иу0 — проекции вектора начальной скорости; т — масса; g — ускорение свободного падения; / — время. Векторы скорости должны исходить из точек, принадлежащих траектории движения тела. Если его начальное положение совпадает с началом координат, то траектория движения описывается законом: 2т Выберем параметры задачи так, чтобы при иа0 = 0.5, му0=0.8 продолжительность полета составила две секунды до падения тела на поверхность, и проследим за изменением его скорости через каждые 0.2 секунды » t = 0:0.2:2; Запишите координаты тела в эти моменты времени в массивы х и у, а проекции скоростей на оси в их и иу: » х = 0.5*t; » у = 0.8*t.*(l - 0.S*t); » их(1:length(х)) = 0.5; » иу = 0.8* (1 - t); Для визуализации поля скоростей вызовите функцию quiver, указав в качестве первой пары входных аргументов массивы х и у с координатами начальных точек векторов, в качестве второй — векторы их и иу со значения- мл проекций векторов скоростей и масштабирующий множитель 0.5 последним пятым аргументом: » quiver(х, у, их, иу, 0.5) Получается наглядная картина движения тела, изображенная на рис. 3.51. В нашем примере функция quiver изображает векторное поле, заданное на кривой линии. 05 0.4 0.3 0.2 01 0 -0 1 -0 2
0.2 0.4 0.6 0 В 1.2 1.4 Рис. 3.51. Зависимость скорости тела от времени (функция quiver) Обратите внимание, что векторы масштабируются, их длины на графике не совпадают с реальными значениями. Во-первых, автоматического масштабирования можно избежать, указав в качестве пятого аргумента ноль » quiver(х, у, их, иу, 0) Во-вторых, можно оставить автоматическое масштабирование, но указать коэффициент увеличения (или уменьшения) длины векторов после него. Сравните: » quiver(х, у, их, иу, 1.5) » quiver(х, у, их, иу, 0.3) Функция quiver допускает замену стрелок, которыми рисуются векторы по умолчанию, на начинающиеся с маркера отрезки. Тип линии, цвет и маркер указываются вместо масштабирующего множителя или после него (т. е. пятым или шестым входным аргументом). » quiver(х, у, их, иу, or—) » quiver(х, у, их, иу, 2.1, *к-.) Подумайте, как отобразить не только векторы скорости, но и траекторию движения в виде плавной кривой. Очевидно, что нужно заново вычислить координаты тела с достаточно малым шагом по времени и использовать команду hold on для наложения линии движения тела на построенный график поля скоростей. Функции compass и feather реализуют другие способы графического отображения векторных полей. Они отличаются от quiver тем, что не требуют задания начальных точек векторов. Функция compass представляет все векторы исходящими из начала координат, a feather — исходящими из равноотстоящих точек на одной прямой. Эти функции удобны, если надо отследить изменение скорости безотносительно к траектории. Вызовите compass и feather, указав в качестве входных аргументов массивы со значениями проекций вектора скорости: » compass(их, иу) » feather(их, иу) Результаты представлены, соответственно, на рис. 3.52 и 3.53. 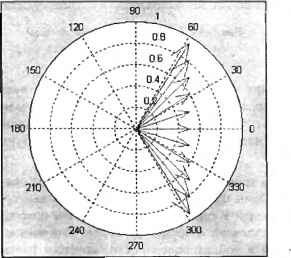 Рис. 3.52. Зависимость скорости тела от времени (функция compass) 0 ... 58 59 60 61 62 63 64 ... 365 |












