Раздел: Документация
0 ... 59 60 61 62 63 64 65 ... 365 Функции compass и feather могут иметь единственный входной аргумент— комплексный вектор, что эквивалентно вызову от двух векторов, первый из которых — вектор вещественных частей, а второй — мнимых. Управление свойствами линий, используемых вместо стрелок, производится так же, как и в quiver. 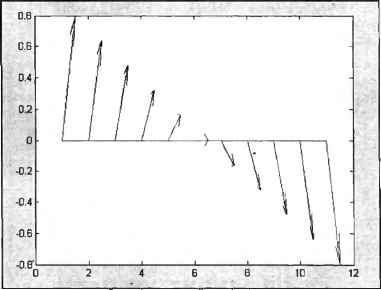 Рис. 3.53. Зависимость скорости тела от времени (функция feather) Полная информация О функциях quiver, compass и feather содержится В интерактивной справочной системе MATLAB и приложении 1. Отметим, что функция quiver может быть использована для визуализации двумерных векторных полей, например, градиента функции (см. пример в справочной системе). Для представления трехмерных векторных полей, заданных на поверхности, служит quiver3. Один из возможных примеров— векторы нормали к поверхности — приведен в справочной системе. Для нахождения нормалей в этом примере привлечена функция surfnorm. Она вычисляет компоненты векторов нормали в точках поверхности, которые соответствуют точкам сетки на плоскости (л% у), генерируемым функцией meshgrid. Изучите пример и самостоятельно постройте внешние нормали к шару радиуса I (рис. 3.54). Проверьте себя: >> u = (-pi:pi/15:pi); » v = -pi:pi/15:pi; » X = sin(u)*cos(v); Y = sin(u)*sin(v); » Z = cos(u)*ones[size(v)); » surf(X, Y, Z) » [U, V, W] = surfnorm(X, Y, Z); » hold on » guiver3(X, Y, Z, U, V,W, 4, k); 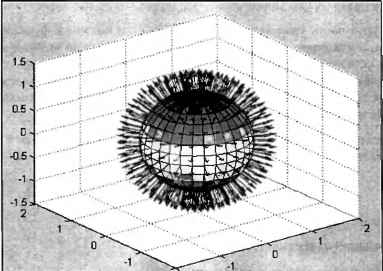 -2 -2 Рис. 3.54. Внешние нормали к шару (функция quiver3) Для изображения трехмерных векторных полей, таких как распределение скоростей в движущейся жидкости или газе, MATLAB предоставляет функцию conepiot. Краткое описание функции дано в приложении 1. Задания для самостоятельной работы 1.Постройте графики функций одной переменной на отрезке [0.01, 2гс]. /(*) = , g(x) = c~xco&x. Выведите графики различными способами: •в отдельные графические окна; •в одно окно на одни оси; •в одно окно на отдельные оси. Дайте заголовки, разместите подписи к осям, легенду, используйте различные цвета, стили линий и типы маркеров, нанесите сетку. Нарисуйте часть графика для отрицательных значений функции синим цветом, а для положительных — красным. Примите во внимание, что на самом деле отображается зависимость одного вектора от другого. Следовательно, можно применить функцию find для поиска индексов требуемых элементов вектора со значениями функции и индексацию вектором для выделения нужных компонент. 2.Визуализируйте функцию двух переменных на прямоугольной области определения z(x,y) = (smx2 + cos>2) , л-е [-1, l], ye [-1, 1]. Выведите графики различными способами: •каркасной поверхностью; •залитой цветом каркасной поверхностью; •промаркированными линиями уровня (самостоятельно выбрать значения функции, отображаемые линиями уровня); •освещенной поверхностью. Расположите графики в отдельных графических окнах и в одном окне с соответствующим числом осей. Представьте вид каркасной или освещенной поверхности с нескольких точек обзора. Отметьте на трехмерном графике точки экстремумов. Используйте то, что значения функции в узлах сетки хранятся в матрице. Определите 0 ... 59 60 61 62 63 64 65 ... 365 |












