Раздел: Документация
0 ... 33 34 35 36 37 38 39 ... 66 В случае проведения анализа по методу Монте-Карло PSpice сохраняет результаты анализа по постоянному току для дальнейшей обработки и сравнения. После того как анализ с номинальным значением параметров завершен, PSpice A/D проводит дополнительные просчеты (например, анализ по постоянному току). Последующие просчеты осуществляются в том же виде анализа, что и просчет номинального варианта, но с принципиальным отличием: вместо использования номинальных значений параметра, просчет производится со значением параметра, определенным с учетом указанных допусков, то есть с новым значением параметра. Имеется выбор при определении количества просчетов при анализе по методу Монте-Карло. Большее количество просчетов обеспечивает более достоверные статистические данные, но при этом требуются большие затраты времени. Количество временных шкал непосредственно линейно связано с количеством просчетов. Во время просчета анализа по методу Монте-Карло PSpice обеспечивает на дисплее индикацию текущего просчета и количество уже выполненных просчетов. По мере того как количество расчетов по методу Монте-Карло возрастает, процесс моделирования требует большего времени и размер файла данных возрастает. Увеличение размера файла данных может привести к замедлению открытия данных и замедлению вывода осциллограмм. Один из способов избежать проявления этого эффекта состоит в том, что необходимо организовать не последовательное выполнение всех просчетов по методу Монте-Карло, а создать блок команд, обеспечивающих каждый раз новое обращение к просчету по методу Монте-Карло. Можно установить набор программных заданий, обеспечивающих построение соответствующих осциллограмм по методу Монте-Карло и оставить выполнение этой задачи на ночь. 4.8.1.Выбор анализа разброса параметров методом Монте-Карло Задача. Из списка возможных видов анализа выбрать анализ разброса параметров методом Монте-Карло (Monte Carlo). Решение. РЕ — D3.AnalysisTypeATime Domain(Transient)[DC Sweep][AC Sweep/Noise], OptionsAMonte Carlo/Worst Case, Monte Carlo, OKI 4.8.2.Настройка и запуск анализа разброса параметров методом Монте-Карло Задача. Перед анализом разброса параметров методом Монте-Карло задать его настройки: выходную переменную число просчитываемых вариантов вид 110 4,8. Анализ разброса параметров методом Монте-Карло распределения (равновероятное либо гауссовское), начальное значение датчика случайных чисел и начать моделирование. Решение. РЕ - D3.AnaIysis TypeTime Domain(Transient)[DC Sweep][AC Sweep/Noise], OptionsAMonte Carlo/Worst Case, Monte Carlo, Output variable->X\ Monte Carlo options, {Number of runs->Y & Use distributionAUniform [Gaussian] & Random number seed->Z, OK - D44 Замечание. Начальное состояние датчика случайных чисел может задаваться в виде нечетных чисел в диапазоне I...32767. По умолчанию оно равняется 17533. 4.8.3. Составление отчета о значениях параметров модели при анализе методом Монте-Карло • Задача. При анализе методом Монте-Карло составить отчет о значениях параметра модели. Решение. РЕ - D3.Analysis TypeTime Domain(Transient)[DC Sweep][AC Sweep/Noise], OptionsAMonte Carlo/Worst Case, Monte Carlo, More Settings.List model parameter value in the output file for each run -> 4, OK, OKI 4.8.4. Создание гистограмм Задача. При анализе по методу Монте-Карло создать гистограммы выходного параметра с псевдонимом X для целевой функции Т. Решение. PS - A6.Axis Settings, Processing Options, Performance Analysis->W, OK -A5.Add Trace, {Function or MacrosAY & Simulation Output Variables}, OKI 4.8.5. Задание количества делений интервала целевой функции для формирования гистограмм Задача. Задать количество делений интервала целевой функции для формирования гистограмм равным N. Решение. PS - A8.0ptions, Number of Histogram Divisions->N, OKI 111 4.8.6. Пример анализа разброса параметров методом Монте-Карло В качестве примера анализа разброса параметров методом Монте-Карло рассмотрим влияние разброса параметров сопротивления R1 на величину коллекторного тока (целевая функция). Схема приведена на рис. 4.14. Численные значения параметров элементов приведены на схеме. Тип анализа — переходный процесс. Распределение случайной величины — гауссовское, число про- R2 10 I-СП-, I— V2 - 10 V1=0 V2=5 TD=10u TR=100n TF=100n PW=1us PER=2s 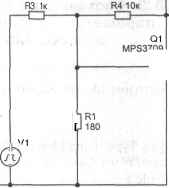 Рис. 4.14. Схема для определения влияния разброса параметров элемента на разброс целевой функции (метод Монте-Карло) р40 с e 20 SEL» 0 16m 20m I I 24m 28m 32m 36m 40m 44m
40mA 30mA 20mA 10mA 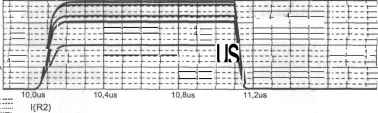 11,6us 11.865us Рис. 4.15. Осциллограммы коллекторного тока (целевая функция) и соответствующая гистограмма 112 0 ... 33 34 35 36 37 38 39 ... 66 |












