Раздел: Документация
0 ... 34 35 36 37 38 39 40 ... 66 счетов целевой функции — 5, допуск на изменение величины сопротивления R1 — 20%, количество делений интервала целевой функции для формирования гистограммы — 10. Осциллограммы коллекторного тока и соответствующая гистограмма приведены на рис. 4.15. Кроме этого на рис. 4.15 приведены численные значения следующих статистических величин: число просчетов целевой функции (n samples), количество делений интервала целевой функции для формирования гистограммы (n divisions), среднее значение целевой функции (mean), среднеквадратичное отклонение целевой функции (sigrna), минимальное значение целевой функции (minimum), десятипроцентная окрестность минимального значения целевой функции (10 %ile), медиана (median), десятипроцентная окрестность максимального значения целевой функции (90 %ile), максимальное значение целевой функции (maximum). 4.9. Анализ чувствительности методом наихудшего случая Анализ чувствительности методом наихудшего случаем используется, чтобы найти наихудший возможный вариант режима работы схемы или устройства с учетом разброса параметров. Например, если рассматриваются три резистора R2 и R3 и допуск на их сопротивление %, при анализе по наихудшему случаю будет найдена комбинация возможных значений сопротивлений, которые обеспечивают наихудший случай и будет проведено для этого варианта моделирование. При анализе чувствительности методом наихудшего случая рассматриваются три важных элемента: вход, рабочая процедура и выход. В дополнение к описанию моделируемой схемы необходимо обеспечить следующую информацию: •допуски параметра; •определение понятия наихудшего случая. Возможно установление допусков на любое количество параметров, которые характеризуют модель. Критерий для определения наихудшего случая, для расположения параметров модели в допустимых пределах их изменения, определяется директивой как некоторая функция базовых выходных переменных при определенном типе анализа. В заданном диапазоне каждый параметр приводится к соответствующему значению с использованием одной из пяти функций (см. табл. 4.4). Наихудший случай определяется как наибольшее (HI) или наименьшее (LO) возможное значение функции по отношению к номинальному значению. Чтобы установить начальное значение функции, по отношению к которой определяется наихудший случай (функция сопоставления), анализ начинается с просчета номинального режима, определяемого номинальными значениями параметров модели. 113
Затем с помощью ряда просчетов определяется индивидуальное воздействие каждого параметра модели на функцию сопоставления. Это осуществляется изменением параметров модели по одному при каждом просчете. Направление (лучше или хуже), в котором изменение функции сопоставления происходит с малым увеличением при изменении каждого параметра модели, регистрируется. Наконец, для просчета наихудшего случая значение величины каждого параметра берется так далеко от номинала, как это позволяет допуск в направлении, которое вызывало изменение функции сопоставления к ее худшему значению (задается максимальным HI или минимальным LO относительным значением функции сопоставления). Анализ нахождения наихудшего случая не является оптимизационным процессом; при нем не происходит поиск набора параметров, которые дают наихудший результат. Это предполагает, что наихудший случай реализуется, когда каждый параметр находится на одном из концов интервала допуска или принимает свое номинальное значение. Наихудший случай выдается, когда функция сопоставления монотонна при всех комбинациях допусков параметров. Обычно уверенности том, что это утверждение истинно, нет, но проведение поиска наихудшего случая указывает на возможность аномального поведения анализируемой цепи. Результаты анализа чувствительности печатаются в выходном файле (.OUT). Этот результат показывает процентное изменение величины функции сопоставления, отнесенное к малым (по умолчанию — 1%) изменениям каждого параметра модели. Если директива .PROBE включена в файл схемы, тогда результаты номинального просчета и просчета для наихудшего случая сохраняются для просмотра в окне Probe. Для каждого изменяемого параметра задаются: изменение функции сопоставления в процентах и значения переменных, в которых заданы значения функции сопоставления. При применении функции сопоставления УМАХ в выходном файле также перечисляются отклонения и среднеквадратичные отклонения значений. Это основывается на изменениях выходных переменных от номинального значения на каждой точке при каждом просчете анализа чувствительности. 114 Таблица 4.4. Функции для определения значения параметра при анализе методом наихудшего случая 4.9.1. Выбор анализа чувствительности методом наихудшего случая Задача. Из списка возможных видов анализа выбрать анализ чувствительности методом наихудшего случая (Worst Case/Sensitivity). Решение. РЕ - D3.Analysis TypeATime Domain(Transient)[DC Sweep][AC Sweep/Noise], Options" Monte Carlo/Worst Case, Worst Case/Sensitivity, OKI 4.9.2. Настройка и запуск анализа чувствительности методом наихудшего случая Задача. Перед анализом чувствительности методом наихудшего случая задать его настройки: выходную переменнуювид допуска (DEV или LOT) и пе- речень типов элементов модели схемы X, участвующих в анализе чувствительности методом наихудшего случая, и начать моделирование. Решение. РЕ - D3.Analysis TypeTime Domain(Transient)[DC Sweep] [AC Sweep/Noise], OptionsAMonte Carlo/Worst Case, Worst Case/Sensitivity, Output Variab-le->TOUT\ {Vary Devices that have" DEV [LOT] [both DEV and LOT] & Limit devices to type(s)->X}, OK - D4l 4.9.3. Пример анализа чувствительности методом наихудшего случая Анализ чувствительности методом наихудшего случая проведен на схеме (рис. 4.16), которая обеспечивает коммутацию биполярного транзистора MPS3709, управляемого от источника напряжения VPULSE. При этом допуск 20% имеют резисторы R1 и R4, а резисторы R2 и R3 являются постоянными (допуск на их изменение не задается). Остальные параметры элементов приведены на схеме. Функцией сопоставления является величина тока через резистор R2.методом наихудшего случая 115 I R2 10 -V2 -10 V1=0 V2=5 TD=10u TR=100n TF=100n PW=1us PER=2s 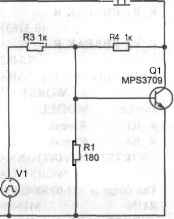 Рис. 4.16. Схема для определения чувствительности 0 ... 34 35 36 37 38 39 40 ... 66 |












