Раздел: Документация
0 ... 89 90 91 92 93 94 95 ... 177 обойтись. Дело в том, что порой встречаются такие уравнения, которые нельзя решить ни аналитически, с использованием оператора solve, ни численно, применяя функцию root Невозможность аналитического решения объясняется сложностью соответству юшнх уравнений. То же, что найти корни этих уравнений невозможно посредством численных методов, связано с тем, что описывающие их функции принимают не непрерывный, а дискретный набор значений. Приведем три примера таких функций: Функция Н(п) определена лишь при целых неотрицательных п, так как только такие значения могут соответствовать порядку производной. Прн аналогичных значениях п су1цествуетй(п), что слизано с тем, что в знаменателе ее выражения вычисляется факториал. Функция f3(n) дискретна, так как она задается суммированием членов ряда от 0 до п, Чтобы решить уравнение графически, следует построить график функции, соответствующей сто левой части. Затем нужно провести вспомогательную линию на уровне, определяемом правой частью уравнения. Область, в которой вспомогательная линия и кривая функции пересекаются, следует увеличить, используя инструмент Zoom (Масштаб) (подробно данный инструмент описывается в главе, посвященной графикам). Если решение нужзго найти максимально точно, эту операцию следует проделать несколько раз. Затем необходимо определить координаты точки пересечения вспомогательной линии и кривой, задействовав инструмент Trace X-Y (Следовать X-Y) при включенном параметре Track Data Points (Следовать точкам данных). Пример 8.20. Графическое решение уравнения Пусть стоит задача с точностью до 10"" найти сумму следующего бесконечного ряда: Так как данный ряд является абсолютно сходящимся, то точность его приближения у сечей и ым рялом не превышает величины первого отброшенного члена. Соответственно, нужно определить, при каком п член ряда принимает значение, меньшее Ю"1*. Сделать это, используя оператор solve или функцию root, не получится. Но эту задачу можно решить графически (рис 8.8). Итак, необходимо просуммировать где-то 15—16 членов ряда. В том, что прн этом будет достигнут» требуемая точность, можно убедиться, вычистив сумму бесконечного ряда аналитически. В отдельных случаях функции дискретного аргумента можно преобразовать в идентичные, но непрерывные функции. При «том становится возможным использование численных И, порой, даже аналитических методов решения уравнении. Так, если в выражении дискретной функции присутствует факториал, то его можно заменить Г-функцией Эйлера. Данная функция является обобщением понятия факториала на всю область действительных чисел. Она непрерывна прн положительных значениях аргумента, принимая при целочисленном значении аргумента те же  п = 0 п=0 п=0 значения, что и факториал. Используя Г-функцню. поставленную выше задачу можно решить проще: root(ifn),n,l,5(J) = 16.256 10 : 1 ь о 1 -щ \-1 ш. Ь I 10 ] 10 j-1 19 \ у № L Ю , h г* ! 10 - 1Ю МО 1 ш . „МО-" ю-имо"к I 10~" Г» у г11 V а 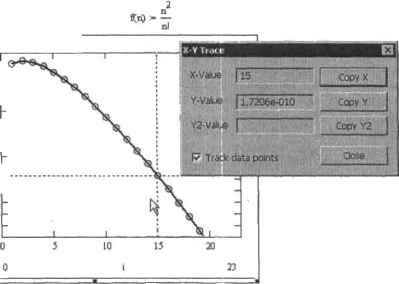 Рис. в.8, Графическое решение уравнения. Так как функция изменяется крайне быстро и ее значения для разных п различаются на много порядков, го на оси Y следует использовать логарифмическую шкалу 8.2. Решение систем уравнений Принципы, лежащие в основе как аналитического, так и численного решения систем уравнений схожи с принципами, па которых основывается решение одинарных уравнений. Поэтому, прежде чем приступить к изучению этого раздела, прочитайте раздел предыдущий. Многие описывающиеся в нем идеи мы не будем повторять в этом разделе, считая, что они уже прочно усвоены. К примеру, мы не будем подробно останавливаться на системной переменной TDL, так ках в случае решения систем уравнений она исполняет ту же роль, что и н случае уравнений одинарных. Данная глава разделена на две части. В первой мы изучим способы решения систем линейных уравнений, во второй — нелинейных, Однако вы должны понимать, что линейные уравнения есть не более чем подмножество нелинейных. Поэтому способы решения систем нелинейных уравнений могут быть использованы для решения систем линейных уравнений. Однако на практике проще использовать специализированные средства решения линейных уравнений, так как при этом не придется задавать! анальные приближения, а ответ будет получен быстрее и точнее. 8.2.1. Решение систем линейных уравнений Все методы решения систем линейных алгебраических уравнений можно разделить на две основные группы. К первой относятся гак называемые прямые методы, например. Крамера или Гаусса, Во вторую группу входнтдовольноспецифичные итеративные методы. В системе Mathcad реализованы методы обеих групп. При использовании прямых методов расчет можно вести как численно, так н символьно. Итеративные методы применяются лишь в численных расчетах. Наиболее просто можно решить систему линейных уравнений, bchomithb некоторые правила линейной алгебры. Нижележащий пример демонстрирует аналитическое и численное решение системы уравнений с использованием обратной матрицы. Пример 8.21. Решить систему линейных уравнений следующего вида: x+y + z+ p=10 x-y-z-p = -8 x+y-z+p=4 -х - у + z + р= 4 Прежде всего следует переписать систему в матричном виде. Для этого нужно состапить матрицу коэффициентов, вектор неизвестных и вектор правых частей. * \ V 1 1 I -J -1 -1 11-11 Ы -1 1 1) KOF
Теперь данную систему уравнений можно заменить тождественным ей матричным выражением KOF-X-PR. В справедливости его можно убедиться, яы ноли и н матричное умножение. Чтобы выразить вектор решений, умножим слева обе части уравнения па матрицу,обратную KOF, В результате получим конечную формулу X-KOF-PR, по которой и будем вести расчет. KOF l-PR (О 2 3 KOF -PR « 2 3 Находить решение системы линейных уравнений через обратную матрицу вполне допустимо, если количество уравнений в системе невелико и расчет должен быть произведен только один раз. Если же система большая пли же одновременно нужно решить много систем, то такой подход tie является оптимальным. В Mathcad встроен более быстрый и точный метод решения систем линейных уравнений, основанный на LU-разложении (о его сути мы поговорим чуть ниже). Чтобы его использовать, следует обратиться к встроенной функции Isolve(M.v), гдеМ — матрица коэффициентов, v — вектор правых частей. Расчет данная функция может вести как численно, так и аналитически. 0 ... 89 90 91 92 93 94 95 ... 177 |












