Раздел: Документация

0 ... 46 47 48 49 50 51 52 ... 87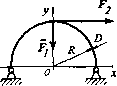

J»-

При формировании элемента PIPEJ8 необходимы три узла: два граничных и уз ределяющий положение центра кривизны элемента.0l1

В качестве примера рассмотрим стержень круглого поперечного сечения диаметр, D = 2 см, согнутый в виде полукольца радиусом R = д* и нагруженный в своей плоскости радиальной J*! Fj = /00 кГ и тангенциальной силой F2=lSQl(p (рис. 3.10 а).

Для построения эпюр на криволинейных стерли можно использовать команду PLLS. Напомним, чтоГ команде PLLS набор линейных эпюр строится на линии соединяющих узлы элементов. Поэтому для более точное картинки эпюр нужно дополнительно сгенерировать Рис.3.10, аи элементы. Чем мельче будут элементы, тем лучше буду,

выглядеть и получающиеся эпюры. Следует также отметить, что при рисовании плоской системы кривых стержней в плоскости Оху, в соответствии с документацией по элементу PIPE 18, поперечные силы в узлах будут находиться в позициях SMISC.3 и SMISC.9 (как MFORZ), а изгибающие мо. менты— в позициях SMISC.5 и SMISC.11 (как MMOMY) элементной таблицы ETABLE. Это также отличает процедуры рисования эпюр для элементов PIPE 18 от рассмотренного ранее случая с элементами ВЕАМЗ. Соответствующая программа CURVED BAR 2, в основе которой лежит программа для расчета криволинейных стержней из [16], приводится ниже:

/batch! пакетный режим /batch

/title, curved bar 2 ! заголовок: кривой брус 2

/show, curved bar 2,grph ! задаем вывод графики в файл curved bar 2.grph

/ргер7 ! входим в препроцессор /ргер7, все данные в системе СГС

dr = 2! dr—диаметр стержня

аг = 20! аг — радиус кривизны

et,l,pipel8! КЭ — искривленные трубки PIPE18

г, 1 ,dr,dr/2,ar ! константы элемента PIPE 18: внешний диаметр

! сечения OD = dr, толщина стенок трубы tkwall = dr/2 ! (сплошная труба), радиус кривизны radcur = аг

mp.ex, 1,2е6! модуль Юнга ЕХ= 2 10**кГ/ см2

mp,nuxy,.3! коэффициент Пуассона NUXY =

п Ш1 = 20! число дополнительных узлов на каждом участке в 90 0

csys.l! переходим в цилиндрическую систему координат

n,i! определяем узлы по координатам

п,2,аг,180

n,2+n fill,ar,90

fill,2,2+n fill,n fill-l ! генерируем п Jill-1 равноотстоящих узлов ! между узлами 2 и 2+п Jill

n,2+n fill*2,ar

fiU,2+n fill,2+n fill*2i fill-l ! генерируем n fill-l равноотстоящих узлов

! между узлами 2+n Jill и 2+пJill*2 csys.O! возвращаемся в декартову систему координат

*do,i,2,l+n fill*2 е,М+1,1 *enddo finish

/solu! входим в решатель /solution

antype.static ! статический тип анализа d,all,uz,0

d,2,ux,0 $ d,2,uy,0 ! задаем условия закрепления в узлах

---

л 2+п п11*2,их,0 $ d,2+n fill*2,uy,0

f2+nJM,fy>-100 задаем силу F; = 100 кГ в узле

f 2+п fill,fx, 150 ! задаем силу Fj = 150 кГ в узле JUI

solve finish

I согласно документации по КЭ PIPE18

! определяем указатели на значения нормальных и поперечных сил и i изгибающих моментов иа концах элементов

etable,mforxi,smisc, 1 etable,mforxj,smisc,7 etable,mforyi,smisc,3 etable,mforyj,smisc,9 etable,mmomzi,smisc,5 eiable,mmornzj,smisc,l 1 /output, curved bar 2,res prrsol

pretab,mforyi,mforyj pretab,mforxi,mforxj pretab,miromzi,rrunomzj /output /pnum,node,l pldisp.l eplot /pbc,u,,l /pbc,f„l /pbc,m,,l /psf,pres,norm,l /pnum,elem,l /pnum,node,0 /number,!

smisc, 1 — нормальная сила N в узле i smisc, 7 — нормальная сила N в узле j smisc,3 — поперечная сила Q в узле i smisc,9 — поперечная сила Q в узле j smisc,5 — изгибающий момент М в узле i smisc, 11 — изгибающий момент М в узле j направляем вывод в файл curved bar 2.res печатаем опорные реакции печатаем поперечные силы печатаем нормальные силы печатаем изгибающие моменты

! нумеровать узлы при графическом показе ! показ деформированной формы стержня ! нарисовать элементы

! показывать граничные условия, силы и моменты

! показывать распределенные нормальные нагрузки ! нумеровать элементы ! ие нумеровать узлы ! занумерованные объекты показывать ! только различным цветом без нумерации ! масштабировать окно для удобства ! ие показывать граничные условия, силы и моменты ! ие показывать распределенные нагрузки ! ие нумеровать элементы ! ие показывать начало и систему координат ! графический показ эпюры поперечных сил Q ! графический показ эпюры нормальных сил N plls,tranomzi,mmomzj,-2 ! графический показ эпюры изгибающих моментов М finish /exit

/zoom, l.scrn,,, 1.7

/pbc,all„0

/psf,pres,norm,0

/pnum,elem,0

/triad,off

pUs,mforyi,mforyj ,2 plls,mforxi,mforxj,2

На рис. 3.10 6-д приведены результаты, полученные по программе CURVED BAR 2. 3.10 б иллюстрирует деформированную форму бруса, а иа рис. 3.10 в-д приведены, соответствеиио, эпюры перерезывающих сил, нормальных сил и изгибающих моментов.

3.1.8. Начальные деформации

Начальную относительную деформацию для стержневых и балочных элементов типа UNfC и BEAM можно задать как константу 1STRN элемента в разделе Real Constant. Для 3аДач сопротивления материалов с начальными деформациями характерно наличие жест-*°го элемента конструкции. Жесткая часть конструкции ие должна деформироваться и, Довательио, ие может состоять из стержневых или балочных конечных элементов. Од-Яко она накладывает ограничения иа перемещения узлов коиечно-злементной модели в

---

виде некоторых уравнений связей. В ANSYS узловые перемещения можно уравнениям связей (constraint equation), используя команду: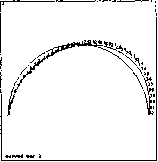

VL0X КО, I

им

*urr**e

CMC >,t№tU XV -1

»

Puc.3.10, б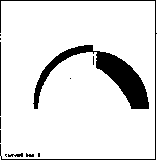

9L&f so. *

uwt имя*

W* *-]«.40<S сиси*»

-пе.мз

«,»84

ж» —ш,т

НИХ »**»,*>»*

-

-ПС, (.4 Ш.Ш

4«.«t

Рис.3.10, г

Рис.3.10, д

Command(s):

СЕ, ЛЖе/V, CONST.NODEl.Labl, CJ,NODE2,Lab2, C2,NODE3,Lab3, СЗ

GUI:

Main Menn —> Preprocessor —> Conpling / Ceqn —> Constraint Eqn

Здесь NEQN— ссылочный номер уравнения связи, Labi, Lab2, Lab3 — обозначения перемещений в узлах NODE1, NODE2 и NODE3 соответственно, и уравнение имеет вид: CONST = Labi *С1 +Lab2 *C2+Lab3 *СЗ.

В качестве примера рассмотрим следующую задачу (рис. 3.11).

Жесткий брус подвешен иа три стальных стержнях с одинаковым попе-

речным сечением площадью 25 СМ каждый расположенных иа расстояния» ах =100 СМ друг от друга. Стержень 3 имеет длину а у = 100 СМ-Стержень 2 короче стержня 3 и8 82=0,05 см, а стержень 1 коро* стержня 3 иа Sj =0,06 см. Требуете определить напряжения в стержнях после сборки всей конструкции.

I®

4~H< bits

Ф б

Т

Рис.3.11

0 ... 46 47 48 49 50 51 52 ... 87