Раздел: Документация
0 ... 52 53 54 55 56 57 58 ... 87 I/EDGEl [/СЫНЕ] Edgo Option* UNWindow nuabor [/EDGE] Plot elatent outlines Edge tolerance angle [/GLIMEl Elenant outline «tyl« □ "3 jEdges only "3 non-contour/contour plots Dashed / Solid j] LOT) Replot upon OK/Apply? Rt-plot 3 I Apply а)выбрать Edges Oni„ [/EDGE] (показывать 8 границы областей); blt(> б)выбрать Dashed/So (сплошными линиями); " в)выбрать Replot(o6a(, вить картинку после вып0 нения команды);л" г)ОК. Просмотр списка значений усилий в граничных узлах Применяя метод конечных элементов, необходимо иметь возможность контролировать правильность решения. Так, например, в данной задаче сумма реакций в узлах в направлении оси у должна равняться приложенной силе, а в направлении осн X — нулю. Приведенная ниже операция позволяет вывести в текстовой форме значения компонентов сил в узлах, лежащих на границах области: Main Menn—>General Postproc-*- List Resnlts-+Reaction Soln а)OK (просмотр всех реакций в появившемся окне); б)Close. 3.2.1.5. Выход из ANSYS. При выполнении процедуры выхода можно сохранить данные в различном объеме: геометрия и граничные условия (save Geom + Loads); геометрия, граничные условия и параметры расчета (save Geom + Loads + Solu); геометрия, граничные условия, параметры расчета и результаты (save Every-thing); ничего (No Save!): Tool bar -»Qnit а) выбрать последний пункт; б)ОК. 3.3. Пространственные задачи 3.3.1. Толстостенный цилиндр под внутренним давлением Ниже приводится пример трехмерного моделирования н решения пространственной задачи определения напряженно-деформированного состояния длинного толстостенного стального цилиндра, находящегося под действием внутреннего давления. Продольное сечение цилиндра и система координат показаны на рнс. 3.15 а, б (размеры в мм). Учитывая симметрию задачи, будем рассматривать лишь четверть цилиндра высотой 1 см. V? 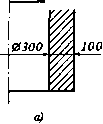
Рис.3.15 б) (]рв)сгИчесКОе 1ГОИменение MeToaa конечных элементов175 {Сонечнс-элементную модель строим посредством поворота на угол РОпрямоуголь- указанных на рис. 3.16 6 размеров вокруг продольной оси у. Задачу решаем в система Механические свойства стали: модуль упругости Е- 2-10 Па, коэффициент Пуассона V = . Внутреннее давление Р = 106 Па(10атм). решение задачи выполняем в интерактивном режиме (GUI). Поскольку первые шаги ..процессорной подготовки и построения модели в данной задаче аналогичны соответ-,уюшим шагам задачи, приведенной в п. 3.2.1, здесь они лишь перечисляются и подробно не рассматриваются. 3.3.1.1. Создание модели Ввод имени задачи: Utility Мепп —> File -»Change jobname а)ввести: Cylinder, б)нажать: ОК. Вод заголовка: Utility Мепи -» File -» Change Title а)ввести: Cylinder under pressure; б)нажать ОК. Установка фильтров: Main Menu —> Preferences а)нажать кнопку: Strnctnral; б)ОК (выбрали задачу механики деформируемого твердого тела). Выбор типа элементов В данной задаче выбирается трехмерный тетрагональный элемент с 10 узлами SOLID92: Main Menu —> Preprocessor -» Element type -» Add / Edit / Delete а)нажать: Add (добавить новый тип элемента); б)выбрать в библиотеке элементов (левое окно) Solid; в)выбрать lOnode 92 в окне Selection; г)Close. Свойства материала В данном примере задается изотропный материал с постоянными свойствами: Main Menu —> Preprocessor -+ Material Props -+ Constant - Isotropic а)OK (набор свойств для материала №1); б)ввести 2.е11 в ЕХ (модуль упругости); в)ввести 03 в NUXY (коэффициент Пуассона); г)ОК для закрытия окна. Создание прямоугольника В данной задаче модель создается прн помощи геометрических "Римитивов и автоматического построения сетки. Прямоугольные "Римитивы можно построить, например, по координатам одного из Углов прямоугольника в глобальной системе координат, его ширины н "Ысоты: Main Menn —> Preprocessor -» -Modeling - Create -* -Areas - Rectangle —>By 2 Corners (прямоугольник по двум углам) а)ввести 0.15, 0., 0.1 и 0.01 для WP X, WP Y, Width и Height, соот->егственно; б)ОК. Таким образом, прямоугольник, соответствующий элементу сече-будущего цилиндра (рис. 3.16 б), построен.  Вращение прямоугольника, образование цилиндра Для установления оси вращения создадим две ключевые точки на оси Y. Так как чевые точки с номерами 1, 2, 3 и 4 уже существуют (они были созданы при постоо110-прямоугольника), то новым ключевым точкам присвоим номера (с запасом): /д1"*1 Ключевые точки создадим с помощью команды К, записывая ее в поле Pick a menu iilj1 enter an ANSYS command:m°f
К,10,0.,0.,0. Нажать Enter. Определяет ключевую точку номер 10 (0,0,0); К,11,0.,0.2,0. Нажать Enter. Определяет ключевыю точку номер 11 (0,0.2,0). Вращение прямоугольника: Preprocessor ~* -Modeling- ~* Operate ~* Extrude ~* Areas ~* About Ахв а) отмечаем курсором прямоугольник, который требуется вращать; б)ОК; в)отмечаем курсором ключевые точки 10 и , определяющие ось вращения; г)ОК. В появившемся окне Sweep Areas about Axis (Диапазон вращения площади вокруг оси) вводим 9(Р (угол вращения прямоугольника) и нажимаем: ОК.  fiteill]Ui* Ш>rc La«th tN 4««rvc» КТ»N.. *f ••!»*, .«реям На рисунке показана построенная таким образом четверть цилиндрического кольца. Заметим, что для удобства дальнейшей работы построенную модель можно вращать, используя комбинации клавиш <Ctrl + правая кнопки мыши> или панель Pan, Zoom, Rotate в меню PlotCtrls. 3.3.1.2.Построение сетки тетрагональных элементов При создании сетки конечных элементов используем тетрагональный элемент Solid92 с установками по умолчанию: Preprocessor ~* -Meshing- ~* Mesh ~* Volumes ~* Free 3.3.1.3.Получение решения Этап решения начинается с задания граничных условий, а также указания метода и параметров расчета.  Cylinder under pressure 0 ... 52 53 54 55 56 57 58 ... 87 |
||||||||||||||||||||||||||||||












