Раздел: Документация
0 ... 22 23 24 25 26 27 28 ... 122 1М«4Ш1М ш1м1Э41м 1Э41М1М1Э4 1М1М1Э41М  1 коэффициент2 коэффициента  3 коэффициента5 коэффициентов Рис. 3.31. Блок, ограниченный одним (а), двумя (б), тремя в и пятью (г) коэффициентами. 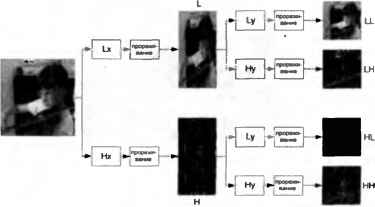 Рис. 3.32. Процесс двухмерного веивлетного разложения.  Рис. 3.33. Изображения после первого шага разложения. Этот подход можно обобщить для применения к двухмерным сигналам, содержащим сэмплированные изображения (рис. 3.32). Каждая строка двухмерного изображения фильтруется низкочастотным и высокочастотным фильтром (L и Н Выход каждого фильтра прореживается с шагом 2. при этом получается 4 субизображения (LL, LH, HL и НН). Эти четыре «субполосных» изображения можно объединить так, чтобы получить ровно столько же сэмплов, что и в исходном изображении (рис. 3.33). LL — это исходное изображение, из которого удалены высокочастотные составляющие по горизонтали и вертикали и сделано прореживание с шагом 2; HL — это высокочастотная составляющая по горизонтали и оставшаяся низкочастотная составляющая по вертикали: LH низкочастотная составляющая по горизонтали и высокочастотная составляющая по вертикали и. наконец, НН высокочастотные составляющие и по 3.4.2.3. Вейвлеты Популярное веивлетное преобразование, широко используемое при сжатии изображений, основано на семействах фильтров с коэффициентами, которые эквивалентны дискретным веивлетным функциям [4]. Основная операция дискретного вейвлетного преобразования применяется к дискретному сигналу, состоящему из N последовательных сэмплов. Пара фильтров применяется к сигналу для его разделения на две составляющие: низкочастотную подполосу (L) и высокочастотную подполосу (Н). Каждая подполоса прореживается через один элемент, и в каждой последовательности частот остается по N 2 сэмплов. При правильном выборе фильтров такая операция является корректной. Риг. 3.34. Два шага воивлотного разложения. 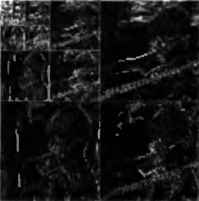 Риг. 3.35. Пять шагов всивлгтного разкимния При использовании в приложениях компрессии данных описанное выше двухмерное вейвлетное разложение повторно применяется к части LL, из которой формируется четыре новых субполосных изображения. Эта процедура многократно повторяется примени- горизонтали, и но вертикали. Эти четыре субполосы содержат в себе всю информацию об исходном изображении, но разреженная структура LH, HL и НН делает их удобными для сжатия. 0 ... 22 23 24 25 26 27 28 ... 122 |












