Раздел: Документация
0 ... 83 84 85 86 87 88 89 ... 166 Важность учета пластических деформаций определяется тем, что их вклад в удлинение образца до его разрушения несоизмеримо больше, чем вклад упругих деформаций. Однако, очевидно, что прежде чем проводить расчеты, необходимо определить модель пластического деформирования. Как и в случае с упругими деформациями, рассмотрим более детально процесс деформирования цилиндрического образца при одноосном на-гружении (осевом растяжении). В этом простейшем случае будем предполагать, что материал является изотропным (рис. 226). Как обсуждалось выше, зависимость напряжений а от деформаций е для металлов (и большинства машиностроительных материалов) вначале имеет линейный или очень близкий линейному участок. Величина напряжений, за пределом которых линейная связь между деформациями и напряжениями нарушается, называется пределом пропорциональности а„ц. Таким образом, до напряжения апц выполняется закон Гука, и деталь после снятия нагрузки возвращается в исходное состояние (геометрическую форму). При превышении, действующим в образце напряжением значения ащ закон деформирования перестает быть линейным. При этом некоторые материалы имеют выраженную площадку текучести (см. рис. 226) (напряжение ат остается постоянным при увеличении деформаций), а некоторые - нет. Однако в обоих случаях важно лишь то, что деформации образца уже состоят из обратимых деформаций ее (см. рис. 226, точка А), которые исчезнут после снятия нагрузки, и пластических (остаточных) деформаций ер, остающихся у образца после снятия нагрузки. Даже если материал не имеет выраженной площадки текучести, то в качестве предела текучести ат выбирается условный предел текучести -определенный уровень напряжений, соответствующий некоторому критическому значению остаточной деформации образца. Выберем на диаграмме точку А. При разгрузке образца зависимость между напряжениями и деформациями носит линейный характер, причем наклон, соответствующей прямой такой же, как и на первоначальном участке (линия, проходящая через точку А и параллельная начальному участку нагружения). Таким образом, при разгрузке материал ведет себя как упругий. Если образец после полной разгрузки снова нагрузить растяжением, то линейный участок будет продолжаться до больших значений, т.е. ощ и ат возрастут. Это явление называется наклепом. Однако, если этот образец повторно (после пластической деформации) сжать, то предел пропорциональности с?" и 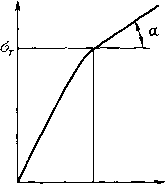 предел текучести о" образца при сжатии уменьшатся по сравнению с соответствующими пределами предварительно недеформирован-ного материала. В этом состоит суть эффекта Баушингера. Отметим, что если при этом выполняется равенство ат + с?" = 2 от, то материал называют циклически идеальным. Это равенство означает, что для пластически деформируемого образца, предел текучести при растяжении увеличивается на- 0 ете Рис. 227. Диаграмма Прандтля столько, насколько он уменьшается Теория пластичности устанавливает связь между напряжениями и деформациями или скоростями изменения деформаций в области пластичности материалов. Очевидно, что решение задач с учетом пластичности гораздо сложнее линейных задач теории упругости. Поэтому в ряде случаев для изотропных тел используются некоторые упрощения связи 8 ~ о для реального материала. Часто в технических расчетах диаграмму растяжения аппроксимируют в виде кусочно-ломаных прямых или так называемых диаграмм Прандтля (рис. 227). Наиболее простой является аппроксимация диаграммы растяжения образца двумя отрезками (в ANSYS билинейная аппроксимация BK.IN и BISO), либо диаграммой, не имеющей выраженной площадки течения (0 < tga < ЕХ , где ЕХ - модуль упругости), либо диаграммой для идеально пластичных материалов (а = 0, например, цветные металлы, железо). Если изотропный материал имеет более сложную диаграмму, либо исследователь хочет более точно отразить участок перехода упругих деформаций в пластические, то используется аппроксимация диаграммы с помощью ломаной, содержащей два и более прямолинейных участка (в ANSYS многолинейная аппроксимация MK.IN и MISO). Замечание! Напряжение текучести для любого металла после технологической обработки точно определяется исходя из испытаний на твердость по Бринеллю. при сжатии. Наличие необратимых деформаций является коренным отличием нелинейных пластических деформаций от нелинейных упругих. При этом нелинейно-упругодеформируемые материалы, как правило, вообще не имеют значительного (с практической точки зрения) линейного участка связи напряжений и деформаций. А пластичность практически всегда (в прикладных исследованиях) рассматривается как продолжение деформирования за пределами упругости. Билинейное кинематическое упрочнение Билинейное кинематическое упрочнение предполагает, что материалы циклически идеальны (см. предыдущий раздел), и учитывает эффект Баушингера. Переход изотропных материалов из упругого состояния в пластическое определяется критерием Мизеса. Замечание! Экспериментально установлено, что модель удовлетворительно описывает деформации большинства металлов. Поведение материалов описывается билинейной кривой деформирования, начинающейся в начале координат с положительными значениями деформаций и напряжений. Наклон первого участка кривой определяется исходя из упругих характеристик материалов. В точке с указанным пользователем значением предела текучести, кривая продолжается вдоль второго угла, определяемого касательным модулем, имеющим те же единицы, что и модуль упругости. Касательный модуль не может быть меньше нуля и больше модуля упругости. Выбор данной модели деформирования осуществляется с помощью следующего пункта в окне Define Material Model Behavior: Material Models Availeble > Steructural > Nonlinear > Inelastic > Kinematic Hardening > Bilinear При использовании этого пункта главного меню, если упругие свойства изотропного материала (модуль упругости и коэффициент Пуассона) с текущим номером не были определены ранее, система ANSYS делает замечание (рис. 228): For trte material model you have to specify elastic properties first, OK 0 ... 83 84 85 86 87 88 89 ... 166 |












