Раздел: Документация
0 ... 14 15 16 17 18 19 20 ... 290 лывающие напряжения имеют на уровне нейтрального слоя. Сопротивление бетона скалыванию в 1,5-2 раза выше, чем осевому растяжению. Таким образом, механическая прочность бетона при различных силовых воздействиях имеет приблизительно следующие значения: при сжатии кубиков.........:.................................. R при сжатии призм..............................................(0,7-0,8)R при осевом растяжении....................................... (0,05-0,1)R на растяжении при изгибе.................................... (0,1- 0,18)R <при чистом срезе................................................ (0,15-0,3)R !при скалывании ................................................. (0,1-0,2)R 2.1.3. Деформации бетона под нагрузкой. Модуль упругости (деформаций) При однократном загружении бетонного образца сжимающей нагрузкой диаграмма напряжения-деформации имеет криволинейный характер, деформации в бетоне растут быстрее напряжений (рис. 2.4, а). В бетоне под действием нагрузки одновременно с упругими развиваются также неупругие деформации, обусловленные ползучестью бетона, т.е. его способностью деформироваться во времени даже при неизменной 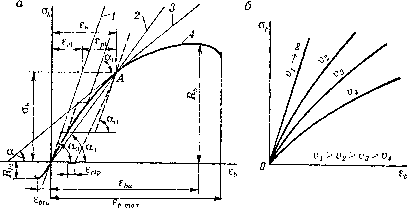 Рис. 2.4. Диаграммы напряжения-деформации бетона при сжатии: 1 - упругие деформации; 2 - секущая; 3 - касательная; 4- полные деформации нагрузке. Опыты показали, что причиной отклонения диаграммы напряжения-деформации для бетона от прямолинейной зависимости Гука является фактор времени. При «мгновенном» загружении деформации бетона следуют закону Гука и зависимость становится линейной. Такая прямая касательна к действительной диаграмме о-е в начале координат, а тангенс угла наклона ее к оси абсцисс представляет собой модуль упругости бетона Eb=tga0=- (2.1) Если образец загружают ступенями, причем после каждой ступени нагрузки образец выдерживают некоторое время при неизменном напряжении, то диаграмма oh-Eb примет ступенчатый характер (рис. 2.4, а, пунктир). Наклонные линии будут выражать развитие упругих (мгновенных) деформаций, пропорциональных напряжениям, а горизонтальные площадки - неупругие деформации, вызванные ползучестью бетона за время выдержки при постоянном напряжении, соответствующем данной ступени загружения. Таким образом, полная деформация бетона еь в любой момент времени представляет собой сумму упругих (проекции наклонных линий на ось абсцисс) и неупругих деформаций (горизонтальные участки диаграммы), т.е. = +(2.2) С уменьшением скорости загружения или увеличения времени выдержки бетона под нагрузкой деформации ползучести возрастают и, следовательно, возрастают и суммарные деформации бетонагь. При этом кривые оь-еь все больше отклоняются от прямой, соответствующей мгновенному загружению (рис. 2.4, б). При разгружении образца криваяаь-еь будет обращена выпуклостью в противоположную сторону, причем касательная к этой кривой, проведенная в точке начала разгрузки (рис. 2.4, а), будет параллельна прямой упругих деформаций при загружении. После полной разгрузки в образце сохраняются (невосстанавливающиеся) деформации, которые, однако, с течением времени частично восстанавливаются. Эта незначительная часть остаточных деформаций (10-15%) называется деформацией упругого последствия (Еф). С увеличением напряжений вследствие развития во времени деформаций ползучести угол наклона касательной к кривой аь-&ь будет уменьшаться. Если провести касательную к этой кривой, то тангенс угла наклона касательной к оси абсцисс, т.е. величина будет представлять собой модуль полных деформаций или, сокращенно, модуль деформаций бетона. В отличие от начального модуля упругости Еь, характеризующего развитие упругих деформаций ее1, модуль деформаций £"й отражает развитие полных деформаций еь. Однако определение модуля деформаций затруднительно; поэтому для практических расчетов железобетонных конструкций используют введенный В.И. Му-рашевым средний модуль упругопластичности бетона, представляющий собой тангенс угла наклона секущей к кривой полных деформаций при заданном напряжении: 4=№=-(2.4) Модуль упругопластичности бетона может быть выражен через модуль упругости следующим образом: из выражений (2.1) и (2.4) следовательно, (2.5) Отношение упругих деформаций бетона к полным называют коэффициентом упругости бетона: а отношение пластических деформаций к полным - коэффициентом пластичности бетона: Я =-. Очевидно, что 0 ... 14 15 16 17 18 19 20 ... 290 |












