Раздел: Документация
0 ... 271 272 273 274 275 276 277 ... 290 В ребристо-кольцевых куполах (рис. 38.3, б) в общую работу каркаса включены непрерывные кольцевые прогоны, которые пересекают меридиональные ребра и работают не только на местный изгиб, но и воспринимают растягивающие кольцевые усилия, являясь ярусными затяжками в расчетной арочной схеме купола (рис. 38.3, г). Площадь сечения условных затяжек в расчетных схемах арок ребристого и ребристо-кольцевого куполов определяют по формуле 2nF F F3 = znt« ,(38.8) пЕ3 где п - количество ребер в куполе; FK, Ек -.площадь сечения и модуль упругости материала кольца;F3 и Е3 - площадь сечения и модуль упругости материала условной затяжки. Сетчатые купола (рис. 38.4) - это многогранники, вписанные чаще всего в сферическую поверхность вращения. Сетка обычно образуется из 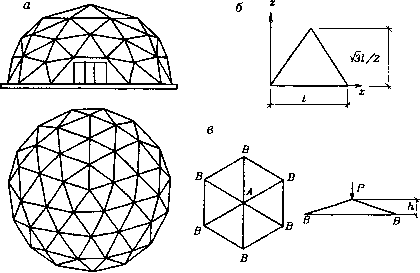 Рис. 38.4. Многогранный сетчатый купол: а - фасад и план; б - к определению усилий в стержнях сетчатого купола; в - к расчету на местную устойчивость треугольников, трапеций, ромбов, пятиугольников, шестиугольников и других фигур. Стержни решетки в узлах сетчатых куполов соединяются шарнирно. Сетчатый купол является распорной системой, распор которой воспринимается нижним кольцом. Наиболее часто применяют купола с треугольной ячейкой. Для сравнительно пологих куполов характерен метод создания сетчатой поверхности, основанный на построении плоской сети для одного из одинаковых пространственных секторов поверхности с последующим проецированием этой сети из центра сферы на криволинейную поверхность купола. Второй метод построения сетчатых поверхностей наиболее выгоден для подъемистых сферических куполов и основан на последовательном членении вписанных в сферу правильных многогранников - додекаэдра (двенадцатигранник) и икосаэдра (двадцатигранник). Элементарные треугольники после членения сферы могут быть объединены в ромбические, пятиугольные, шестиугольные вспарушенные панели. Сетчатые купола рассчитывают по безмоментной теории как сплошные осесимметричные оболочки. Усилия в стержнях купола определяют умножением меридиональных Тх и кольцевых Т2 усилий на соответствующие расстояния между стержнями в рассматриваемых сечениях купола и проектировании этих усилий на направления стержней (рис. 38.4, б). При ячейке в виде равностороннего треугольника усилия в стержнях =-(Щ-Т2);(38.9) N2=(t2-3S);(38.10) где S - сдвигающее усилие в оболочке. Для расчета на местную устойчивость (рис. 38.4, в) необходимо проверить на продольный изгиб стержень купола при расчетной длине, равной /7з (38.12) где гс - радиус инерции сечения стержня; / - длина стержня; h - величина превышения вершины/! пирамиды над примыкающими к нему соседними узлами В (рис. 38.4, в). Чтобы избежать общей потери устойчивости сетчатой сферической оболочки, необходимо, чтобы равномерное радиальное давление на сферический купол не превышало критического =1,6-,(38.13) где Е, F- модуль упругости и площадь сечения стержня, R - радиус сферы. Кружально-сетчатые купола из сомкнутых сводов образуют в плане правильный многоугольник (рис. 38.5), который состоит из одинако- 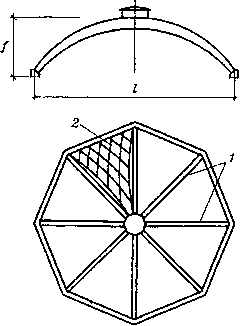 Рис. 38.5. Кружально-сетчатый купол из сомкнутых сводов: 1 - гурты; 2 - сетка из косяков 0 ... 271 272 273 274 275 276 277 ... 290 |












