Раздел: Документация
0 ... 3 4 5 6 7 8 9 ... 290 контролируемое значение ее предела текучести (физического или условного) при растяжении, установленное соответствующими стандартами; за нормативное сопротивление бетона принимаются показатели прочности бетона, заданные с надежностью 0,95. Коэффициент условий работы материалау в формуле (3) учитывает благоприятные или неблагоприятные факторы, возникающие при изготовлении материала и его работе под нагрузкой. Коэффициенты условий работы у, могут быть как больше 1, так и меньше. Значения нормативных и расчетных значений материалов устанавливаются на основании статистической обработки результатов испытаний большого количества образцов. Если при испытании число образцов, показавших прочностьRh составит пь прочность R2 составит п2 образцов и т.д., то средняя прочность всех образцов nlRl+n2R2+-- + nkRk Rm--;---;-•(4) Отложив по оси абсцисс значения прочности Rh R2, R, а по оси ординат - соответствующие числа случаев щ, п2, пь можно построить кривую, получившую название кривой распределения (рис. 7). Из кривой распределения видно, что наибольшее число испытанных образцов показало прочность, равную Rm остальные значения отклоняются от среднего, причем чем больше это отклонение, тем реже оно наблю- ла k 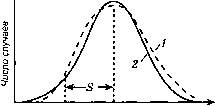 Rmuh RmЛ Прочность Рис. 7. Кривая распределения значений предела прочности материала: 1 - статистическая (опытная) кривая; 2 - теоретическая кривая по формуле (6) дается. Обозначив отклонения прочностей отдельных образцов от среднего значения через Д, = R,-Rm; A2=R2~Rm:...\ Ak=Rk-Rm, определяют среднеквадратичное отклонение, называемое стандартом: Кривая распределения обычно получается симметричной, так как вероятность отклонения прочности как в меньшую, так и в большую стороны примерно одинакова. Она близка к симметричной кривой нормального закона распределения Гаусса-Лапласа где пх - число образцов, показавших прочность Rx; п - общее число образцов; ARX - интервал между значениями Rx. События считается вероятным, если оно проявляется не реже трех раз 3 на 1000 случаев. Ордината кривой распределения, равная наибольшей ординаты, располагается от нее по оси абсцисс на расстоянии 3S. Соответствующая прочность Лшя = Rm - 3S представляет собой практически возможный предел снижения прочности и принимается за расчетное сопротивление. Таким образом, левая часть формулы (1), выражающей идею расчета конструкций по первой группе предельных состояний, представляет собой расчетное усилие, равное практически возможному максимальному усилию в сечении элемента при невыгоднейшей комбинации расчетных нагрузок или воздействий, а правая часть - минимально допустимую несущую способность сечения. Значения усилия N, так же как и несущей способности Ф, зависят от изменчивости указанных выше факторов и, как показывает статистическая обработка наблюдений, подчиняются нормальному закону распределения Гаусса-Лапласа. Выполнение условия (1), выраженного графически на рис. 8, гарантирует требуемую несущую способность с уровнем надежности не менее 0,997. (5) 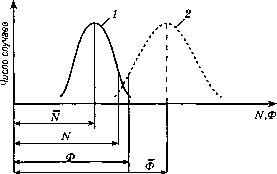 Рис. 8. Распределение значений усилий (1) и несущей способности (2): N и N- среднестатистическое и расчетное значения усилий; Ф и Ф - то же, несущей способности Второе предельное состояние для всех строительных конструкций определяется величинами предельных деформаций, при превышении которых нормальная эксплуатация конструкций становится невозможной. Величины предельных деформаций приведены в нормах проектирования для каждого вида конструкций. Учитывая, что второе предельное состояние обусловливает возможность нормальной эксплуатации конструкций, а также меньшую опасность его возникновения, деформации определяются от действия нормативных нагрузок. При расчете по второму предельному состоянию должно соблюдаться условие А </, где Д - деформация, вызываемая нормативными нагрузками;/- допустимая предельная деформация. К этой же группе предельных состояний железобетонных конструкций относятся расчет по образованию трещин, согласно которому должно соблюдаться условие Mcrc< М, где Мсгс- момент внутренних сил перед образованием трещин, М - момент от расчетных значений внешних сил, а также расчет по ширине раскрытия трещин и их возможному закрытию в предварительно напряженных элементах. Преимущество методики расчета конструкций по предельным состояниям состоит в том, что введение системы коэффициентов (надежно- 0 ... 3 4 5 6 7 8 9 ... 290 |












