Раздел: Документация
0 ... 8 9 10 11 12 13 14 ... 82 Резисторы R7, R8 и транзисторы 77, Т8 введены в схему усилителя рис. 2-8, б для того чтобы обеспечить защиту выхода усилителя от токовых перегрузок. Работает схема защиты здесь точно так же, как рассмотренная выше аналогичная схема в усилителе рис. 2-7, а. В схемах усилителей с повышенной выходной мощностью, приведенных на рис. 2-7 и 2-8, показано подключение входного сигнала, характерное для инвертирующего усилителя. Естественно, что здесь может использоваться и схема неинвертирующего или дифференциального усилителя (см. главу третью). 2-5. Расчет цепей, содержащих ОУ, с помощью направленных графов Направленный граф представляет собой топологическую модель системы линейных уравнений и позволяет наглядно представить влияние различных элементов этих уравнений. Методы составления графов электрических цепей, преобразования таких графов и нахождения по ним токов и напряжений на различных участках цепи разработаны достаточно полно [1, 6, 30]. Поскольку в основе графа лежит система линейных уравнений, то и анализ электрических цепей с помощью графов предполагает наличие такой системы. Для составления системы уравнений удобно пользоваться методом узловых напряжений или контурных токов. Метод узловых напряжений во многих случаях более удобен, поскольку он позволяет непосредственно находить напряжения в различных точках цепи относительно общего узла (земли). На рис. 2-9, а показан участок электрической цепи, прилегающий к узлу, обозначенному буквой /. В соответствии с первым законом Кирхгофа для этого узла можно записать: // + (l/i ~ V,) Уг + (Vt~U,)Yt+ ... + (Vn - Vj) Yn - U,Y0 = 0, (2-2) где I, — ток источника тока, присоединенного к узлу / (задающий ток); Ко — проводимость ветви, соединяющей рассматриваемый /-й узел с нулевым узлом, относительно которого ведется отсчет всех напряжений; Ui, ..., U„, Ki, .. , Yп — соответственно напряжения в различных узлах цепи и проводимости ветвей, соединяющих эти узлы с рассматриваемым /*-м узлом. Исходя из (2-2), для напряжения в /-м узле можно записать следующее уравнение: U, = —L (// + Y±U± + YtUt + . . . + YnUn),(2-3) "h где Kj9= K0 + K1+ ... + Yn — эквивалентная проводимость /-го узла, равная сумме всех проводимостей, присоединенных к этому узлу. Рис. 2-9, б показывает граф цепи рис. 2-9, а, составленный на основании уравнения (2-3). Узлы (вершины) этого графа соответствуют задающему току и узловым напряжениям цепи, а направленные ветви указывают, от каких переменных зависит в данном случае напряжение Vj. Выражения (буквенные или численные), написанные возле ветвей, называются коэффициентами передачи (весами) ветвей и показывают значимость различных переменных в уравнении, соответствующем рассматриваемому узлу. Для графа рис. 2-9, б коэффициенты передачи ветвей — это коэффициенты уравнения (2-3). Коэффициенты передачи всех ветвей графа рис. 2-9, б содержат один и тот же знаменатель У1Э. Для упрощения записи можно условиться этот знаменатель записывать один раз возле обозначения соответствующего узла. Именно так и сделано в графе, показанном на рис. 2-9, в. Следует заметить, что существуют различные типы графов, отличающиеся друг от друга исходными правилами, с помощью которых устанавливают соответствие элементов графа элементам исходного уравнения. В частности, граф рис. 2-9, б соответствует широко распространенному виду графов, назы- ваемых графами Мэйсона. А граф рис. 2-9, в— это так называемый обобщенный сигнальный граф [6]. В обобщенном сигнальном графе выражение, написанное возле кружка, обозначающего узел графа, называется весом узла. Вес узла указывает общий знаменатель всех составляющих, из которых складывается величина, соответствующая данному узлу. Можно также определить вес узла как коэффициент, стоящий перед соответствующим неизвестным в исходном уравнении, на основе которого составлен граф. Это утверждение будет понятно, если уравнение (2-3) переписать так: YhUi=I,+ Y1U1+YtU2+ ... +YnUn. Здесь Узэ — вес узла U, на рис. 2-9, в. При применении метода узловых напряжений вес узла — это собственная проводимость узла. Узлы графа, которые не имеют входящих ветвей, называются истоками (невзвешенными узлами). В обобщенном сигнальном графе истоки обозначают точками и их веса на графе не указывают.  Рис 2-9. Схема участка электрической цепи (а) и соответствующие ей графы для узловых напряжений (бив) Мы в дальнейшем будем пользоваться обобщенными сигнальными графами. Однако, как упомянуто выше, обобщенный сигнальный граф отличается от общепринятого графа Мэйсона только вынесением общего знаменателя входящих в узел ветвей в обозначение веса этого узла. Если это иметь в виду, то нетрудно установить соответствие между правилами, применяемыми в графе Мэйсона, и подобными правилами, применяемыми в обобщенном сигнальном графе. В тех случаях, когда рассматриваемая электрическая цепь содержит много узлов, но мало контуров, целесообразно применять для расчета метод контурных токов. На рис. 2-10, а показан участок электрической цепи, составляющий один /-й контур. Для этого контура в соответствии со вторым законом Кирхгофа можно записать: Е/ + (Л - //) Z1 + (/, - //) Z, -f- . . . + (Ia - //) Z„ - IjZ0 = 0, (2-4) где Ej — э. д. с. источников напряжения вконтуре: h, /г,-.., In — токи контуров, имеющих общие с рассматриваемымконтуром сопротивления Zt, Z2,..., Z„; Z0 — сопротивление, входящее тольков /-й контур. Из (2-4) получаем следующее уравнение: Z/3 // = Ej + Zxlx + Z2I2 + . . . + Z„/„,(2-5) где Zia=Z0+Zi + .. .-j-Z„ — собственное сопротивление контура, равное сумме всех сопротивлений, входящих в /-й контур. Как видим, равенства (2-2), (2-3) и (2-4), (2-5) попарно дуальны друг другу. Граф, соответствующий уравнению (2-5), представлен на рис. 2-10, б. Эквивалентные преобразования графа непосредственно вытекают из соответствующих эквивалентных преобразований системы линейных уравнений. В частности, нетрудно показать, что две соединенные параллельно ветви графа можно заменить одной, коэффициент передачи которой равен сумме коэффициентов передачи исходных ветвей Соединенные последовательно две ветви обобщенного сигнального графа эквивалентны одной ветви, коэффициент передачи которой равен произведению коэффициентов передачи исходных ветвей, деленному на вес узла, стоящего между ними. Введем некоторые определения. Путь — это последовательность однонаправленных ветвей графа. Коэффициент передачи пути равен произведению коэффициентов передачи всех входящих в него ветвей. Замкнутый путь называется контуром. Контур, состоящий всего из одной ветви, носит название петли. Петлю, охватывающую некоторый узел обобщенного графа, можно исключить, уменьшив вес узла на коэффициент передачи петли. 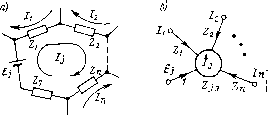 Рис. 2-10 Схема участка электрической цепи (а) и соответствующий ей граф для контурных токов (б) Элементарный граф — совокупность т (т = 0, 1, 2, ...) некасающихся контуров и всех взвешенных узлов графа, через которые не проходят эти контуры. Под некасающимися контурами при этом понимают контуры, не имеющие общих узлов. В составе графа может содержаться достаточно много элементарных графов. Если, например, граф содержит два некасающихся контура, то в нем можно выделить 4 элементарных графа: первый — не содержащий контуров и состоящий только из взвешенных вершин, второй и третий элементарные графы будут содержать по одному контуру и по две взвешенные вершины, а в состав четвертого войдут оба контура. Формула Мэйсона позволяет найти передаточный коэффициент графа от узла р к узлу q: W = 2 Р,- А//А,(2-6) где Р] — коэффициент передачи /-го пути от узла р к узлу q; Д3 —определитель части графа, не касающейся /-го пути; А — определитель полного графа. Таким образом, в числителе формулы (2-6) стоит сумма произведений передаточных коэффициентов всех возможных путей от узла р к узлу q и соответствующих им определителей. Определитель графа равен сумме определителей входящих в него элементарных графов [6]: Л = 26;.(2-7) В свою очередь, определитель элементарного графа вычисляется как произведение весов узлов и взятых с обратным знаком коэффициентов передачи контуров, входящих в этот элементарный граф. Если при нахождении определителя А,, соответствующего /-му пути, выяснится, что в графе отсутствуют узлы, не касающиеся этого пути, то принимается, что Aj= 1. 0 ... 8 9 10 11 12 13 14 ... 82 |












