Раздел: Документация
0 ... 29 30 31 32 33 34 35 ... 82 постоянного тока, полоса пропускания которого распространяется от нуля до некоторой верхней частоты, определяемой постоянной времени Тв эквивалентного инерционного звена первого порядка. 10 дБ/дек  ш0 10дБ/дек Д дБ/дек 20 дБ/дек 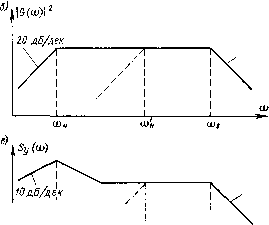 20 дБ/дек ш0 Рис 4-20 Графики, поясняющие распределение мощности шума по частоте в усилителе переменного напряжения Спектральная плотность шума на выходе такого усилителя в первом приближении описывается формулой Sy (со) = K2SX (со)---. Дисперсию выходного сигнала, обусловленную белым и розовым входными шумами, можно найти из формул (4-28), полагая в них 7"н=сс. Соответственно для Dq получим D6=-r.(4-29) 4 Заказ № 319 97 Что же касается £>ф, то оказывается, что эта составляющая дисперсии выходного сигнала для обычного усилителя постоянного тока равна бесконечности. Этот, на первый взгляд, неожиданный результат является следствием того факта, что спектральная плотность фликкер-шума при неограниченном уменьшении частоты стремится к бесконечности. Интересно, что справедливость формулы 5ф(со) = = S0coo/co, из которой следует lim S (со) = оо, подтверждена экспе- ооО риментально при снижении частоты со вплоть до 10~6 с-1. Можно дать следующее объяснение тому, почему все-таки работают усилители постоянного тока, несмотря на то, что, на первый взгляд, они должны быть неработоспособны из-за бесконечной дисперсии шума на выходе. Дело в том, что практически нижняя граница полосы пропускания шумового сигнала таких усилителей не равна нулю. Действительно, время, в течение которого мы работаем с таким усилителем после первоначальной или очередной подстройки начального уровня выходного сигнала, ограниченно (небесконечно). А раз так, то можно показать, что эквивалентная полоса пропускания для шума такого усилителя начинается не с нуля, а с некоторой начальной частоты. Будем считать, что алгоритм коррекции начального уровня выходного сигнала усилителя заключается в том, что в момент коррекции при равном нулю входном сигнале значение выходного сигнала запоминается и затем это значение вычитается из текущего выходного сигнала усилителя. Выше мы говорили о том, что модуль текущей частотной характеристики бДсо) может быть найден как модуль выходного сигнала при воздействии на вход устройства комплексного колебания еш. Выходной сигнал при отсутствии коррекции будет /а Кеш /соГв+ 1 Если принять, что коррекция проводится в момент времени / = 0, то в устройстве коррекции будет запомнен сигнал Ке>№0К /соГв+1 /еоГв+1 Соответственно выходной сигнал усилителя с учетом коррекции будет У1 (0 = У« (0 - у, (°) = * ■(4-3°) Из (4-30) находим модуль ТЧХ \0(М\ = \у1Щ = К-ЩВ.(4-31) Если в (4-31) положить (о = 0, то получим ] Gt (со) = 0; это значит, что коэффициент усиления усилителя на нулевой частоте равен нулю. Таким образом мы подтвердили высказанное ранее положение, что при ограниченном времени t, прошедшем после проведения коррекции начального уровня усилителя, нижняя граница полосы пропускания шумового сигнала не .равна нулю. За счет этого и происходит ограничение дисперсии на выходе усилителя, обусловленной входным фликкер-шумом. Входящая в формулу для дисперсии (4-26) функция 5у(со) = = Sx(co) Gf(co) 2 (эта функция не есть спектральная плотность в обычном понимании) в соответствии с (4-31) будет равна Ss(ffl) = S,H/<»if.(4-32) На рис. 4-21 показаны (в линейном масштабе) графики Sx(co), j Gf (со) ]2 и Sv((o) для этого случая. Штриховые линии на рис. 4-21,6 и в соответствуют усилителю постоянного тока без коррекции. Интегрируя спектральную плотность (4-32) в пределах от со = 0 до со = оо, найдем составляющие дисперсии шума на выходе, обусловленные белым шумом и фликкер-шумом на входе: ЭД = Ч1-е-/гв);(4-33) D4(0 = X2S0(o0 2C+21n-i--e-tlTEi(-L)-ITEi( 1 т\т\ т ,(4-34) где С = 0,5772 — постоянная Эйлера; Ei(x)—интегральная показательная функция, таблицы которой можно найти, например, в [54]. Дисперсия D§(t), обусловленная белым шумом, возрастает от нуля по экспоненте, стремясь к уровню n nS„/C* иб-- (4-35) Дисперсия D$(t), обусловленная фликкер-шумом, при увеличении t также возрастает от нуля, но не имеет установившегося значения. При t>TB закон изменения D$(t) может быть приближенно описан формулой Оф (/) = 2K2S0 (о0 (in jl + С).(4-36) Поскольку обычно работают с усилителем постоянного тока при />7"в, то именно на соотношения (4-35) и (4-36) следует ориентироваться при оценке дисперсии шума на выходе. Сравнивая (4-29) и (4-35), видим, что введение коррекции удваивает дисперсию, вызванную белым шумом. Это понятно: при г>Гв мгновенные значения выходного шума, обусловленного входным белым шумом, можно считать некоррелированными 0 ... 29 30 31 32 33 34 35 ... 82 |












