Раздел: Документация

0 ... 30 31 32 33 34 35 36 ... 82

со значением шума, запомненным в устройстве коррекции, и суммарная дисперсия будет складываться из дисперсий текущего и запомненного значений шума. Рост дисперсии £>ф(/) при увеличении t физически также объясняется тем, что чем

больше прошло времени от

а)

Sx(w)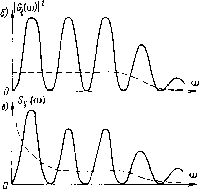

Рис 4-21 Графики, поясняющие распределение мощности шума по частоте в усилителе постоянного напряжения с периодической коррекцией дрейфа

момента запоминания корректирующего сигнала до момента проведения измерения, тем меньше корреляция между зафиксированным и текущим о> значениями шума. Однако го-ворить о равенстве нулю корреляции при t>TB в случае фликкер-шума нельзя, так как в этом виде шума большую долю составляют низкочастотные составляющие.

Формула (4-36), описывающая рост во времени дисперсии D$(t), может быть использована для определения периода проведения коррекций начального уровня выходного сигнала усилителя исходя из допустимой дисперсии шума. Приравнивая дисперсии Dq и D$(t), определяемые соотношениями (4-35) и (4-36), при известных значениях Тв и соо можно найти такой период коррекции t, при котором D<l){t)D6. Получим — с

<7ве2и°Гв .(4-37)

Очевидно, что одновременное выполнение условия (4-37) (соответствующего подавлению фликкер-шума) и условия t>TB (соответствующего окончанию переходных процессов в усилителе после проведения коррекции) возможно только при применении быстродействующего усилителя, когда Гв<с2со0я. При этом необходимо, чтобы и узлы, входящие в устройство коррекции — ключи, устройство запоминания, были также быстродействующими.

Шум усилителя МДМ. Будем рассматривать усилитель МДМ с двухполупериодными модулятором и демодулятором. Структура такого усилителя может быть изображена так, как показано на рис. 4-22 Модулятор и демодулятор здесь условно показаны в виде инвертора с коэффициентом передачи, рав-

---

ным — 1, и двухпозиционного переключателя, присоединяющего к выходу сигнал то непосредственно, то через инвертор. Источник шумового напряжения (Уш условно вынесен за пределы усилителя напряжения У.

Можно считать, что в усилителе по схеме рис. 4-22 осуществляется коррекция начального уровня выходного сигнала в каждом периоде коммутации модулятора и демодулятора. Действительно, входной сигнал усилителя UBx, пройдя через модулятор и усилитель, затем снова восстанавливается по форме в демодуляторе. Так что цепь, состоящая из последовательно включенных узлов М, У, ДМ, просто усиливает входной сигнал в К раз, где К — коэффициент усиления усилителя У. Что же касается шума, то он подается на выход ДМ то непо-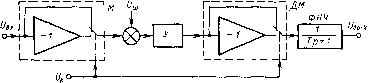

Рис 4-22 Структурная схема к расчету шуморых свойств усилителя

МДМ

средственно, то через инвертор, т. е. демодулятор выступает для шумового сигнала в качестве модулятора. Понятно, что если шумовой сигнал за период коммутации меняется незначительно, то среднее за период коммутации значение сигнала, обусловленного шумом, на выходе ДМ будет близко к нулю. Функцию усреднения в структуре рис. 4-22 выполняет фильтр нижних частот первого порядка с постоянной времени Т. Найдем модуль частотной характеристики для шумового сигнала в усилителе МДМ. Будем считать, что в схеме рис. 4-22 на место источника шумового сигнала (Уш включен источник комплексного гармонического колебания еи. Предполагая, что этот источник действовал начиная с г=—со, для момента времени г = 0, совпадающего с окончанием положительного полупериода коммутации, получим

GoHI =

к e!atet/Tdt

-г„

-к J .

—2Т

к

—2 Г;

+ к

,/(ЙГ

ei/Tdt +

т

(4-38)

где Тк — длительность полупериода коммутации. Весовая функ-

---

ция для ФНЧ в данном случае равна ~jre i/T-Ho поскольку момент времени, для которого мы ищем значение выходного сигнала, соответствует = 0, то в интегралы свертки, входящие

1 — (0—t)/T 1 J/T

в (4-38), весовая функция входит в виде ~ге~~т

Чередование знаков « + » и «—» перед интегралами в (4-38) отражает работу демодулятора.

После взятия интегралов правая часть равенства (4-38) приводится к бесконечной геометрической прогрессии, находя сумму которой, получаем

1G0 (со) = /С

-;шГ - Г Г

е к е к

(4-39)

итТ+1){1 + е-,аТ"в-Т/Т)

Освобождаясь от функций комплексного аргумента и переходя к квадрату модуля частотной характеристики, находим

[l + е"2ТкТ - 2е~ ГкГ cos (юТк)] К2

G0(co)

(to2T2+l) [l+ Г2Гк/Г+ 2(ГГ*Гсо8 (шГк)] [ch (Тк/Т) - cos (соГк) ] К2

-. (4-40) (со2Г + 1) [ch (Тк/Т) + cos (шГк) ] V

График кривой изменения G0 (со) 2, соответствующий формуле (4-40), показан на рис. 4-23. Как видим, амплитудно-частотная характеристика (АЧХ) усилителя МДМ для шума имеет явно выраженные всплески на частотах со = я/Гк, со = Зя/Гк и т. д. Вблизи со = л/Гк кривая АЧХ довольно хорошо совпадает с резонансной кривой, характерной для обычного LC-контура. Действительно, вводя обозначения соо = я/Т

к и учитывая, что при 7к/7<1 можем принять е-г« г « 1—TJT, ёаТ"ж -1 — /АсоГк. где Асо = со—соо, из (4-39) получим

4К2

М- + Лсо

к

т2

п2Г2 / Дм \2

(4-41)

Для резонансного же контура, имеющего добротность Q, АЧХ определяется формулой

G(co)2 =---.(4-42)

1 v п 1 + 4Q2 (Дм/со)2v ;

Сравнивая (4-41) и (4-42), видим, что для шума усилитель МДМ имеет АЧХ, близкую к АЧХ резонансного контура с добротностью Q = nT/ (2ТК).

Вблизи частот kn/Tv, где k — Ъ, 5, 7,..., АЧХ усилителя МДМ имеет всплески, амплитуда которых убывает обратно пропорционально k, в то время как ширина этих всплесков (по уровню 0,7) остается неизменной,

0 ... 30 31 32 33 34 35 36 ... 82