Раздел: Документация
0 ... 58 59 60 61 62 63 64 ... 82 а (Ъ -4- с) •= аЬ 4- ас, а 4- be «■ (я 4- (я 4- б)- Последнее равенство можно получить в результате следующих преобразований: a+bc = a-1 4- be = а (1 +Ь + с) + Ьс = а4-а&4-ас4-Ьс = (в4-Ь)(а4-с), Закон поглощения: a + ab = а(1 4-Ь) = а; а (а + Ь)««а 4-аЬ «= а. Закон склеивания: ab--aba; (a~\-b)(aJrb) = a. Закон отрицания: а-\-Ъ *=аЪ; аЬ*=а-\-Ъ. Еще один вид записи закона отрицания выглядит следующим образом: — a+b = ab; ab = a-\-b. Закон отрицания, часто называемый также правилом де Моргана, справедлив для любого числа переменных: а+b 4-е 4- • • • 4- z = ab с ... г, abc . . . z = aJrb 4-с4- • • • 4-г- Функционально полная система логических элементов — это такой набор элементов, используя который, можно реализовать любую сколь угодно сложную логическую функцию. Поскольку любая логическая функция есть комбинация простейших функций— дизъюнкции, конъюнкции и инверсии, то набор из элементов трех типов, реализующих соответственно функции И, ИЛИ и НЕ, естественно, является функционально полным. Например, функцию ab + ab можно реализовать с помощью двух ячеек НЕ (они нужны, чтобы получить инверсии а и ft), двух ячеек И, необходимых для того, чтобы получить логические произведения ab и аЬ, и ячейки ИЛИ, суммирующей эти произведения. Функционально полные системы могут состоять и из набора элементов, реализующих логические функции, отличные от простейших. В частности, функционально полные системы могут состоять из элементов только одного типа, например реализующих функцию И — НЕ либо ИЛИ — НЕ. Функция И — НЕ, носящая также название функции Шеф-фера, означает следующее преобразование: F = abc . . . . Для того чтобы доказать функциональную полноту набора элементов, реализующих функцию И — НЕ, покажем возможность построения на их основе логических цепей, реализующих простейшие функции. Функцию НЕ, т. е. инвертирование переменной, можно реализовать, если сигнал, соответствующий этой переменной, подать на один из входов цепи И — НЕ, а на все остальные входы подать постоянный сигнал, соответствующий единице: а-\...\ — а. Для образования цепи И достаточно включить последовательно цепь И—НЕ и инвертор: ab — ab. Цепь ИЛИ строится в соответствии с правилом де Моргана: ab = a + b. Таким образом, цепи И — НЕ позволяют реализовать инверсию, конъюнкцию и дизъюнкцию, а следовательно, на их основе можно строить логические цепи для реализации сколь угодно сложных функций. Функция ИЛИ — НЕ, называемая также функцией Пирса или функцией Вебба, означает следующую связь между функцией Р и аргументами а, Ъ, с, ...: Fa + b + c + . . . . Для получения инверсии одной переменной достаточно подать сигнал, соответствующий этой переменной, на один вход цепи ИЛИ — НЕ, а на остальных входах этой цепи поддерживать сигнал, соответствующий логическому нулю. Функция ИЛИ может быть реализована путем инвертирования выходного сигнала цепи ИЛИ— НЕ. Функция И реализуется с помощью ячеек ИЛИ — НЕ на основе закона отрицания a + b = ab. Возможность реализации простейших логических функций свидетельствует о функциональной полноте логических элементов ИЛИ —НЕ. Наряду с названиями функций И — НЕ и ИЛИ — НЕ их называют также соответственно функциями НЕ — И и НЕ — ИЛИ. В зарубежной литературе встречаются также названия NAND (НЕ —И) и NOR (НЕ —ИЛИ), образованные путем слияния английских слов NO — AND (НЕ — И) и NO — OR (НЕ — ИЛИ). В отечественной литературе также используются подобные обозначения: НЕЙ и НЕИЛИ. 10-2. Разновидности логических ИС Логические ИС могут быть построены по-разному, но в их основе, как правило, лежат схемы, выполняющие функции И — НЕ либо ИЛИ — НЕ. Поэтому логическая интегральная схема содержит обычно схему И либо ИЛИ, выполненную на резисторах, диодах или транзисторах, и транзисторный инвертор. Транзисторный инвертор может быть простейшим — на одном транзисторе, включенном по схеме с общим эмиттером, или сложным — многотранзисторным с каскодным включением транзисторов в выходном каскаде. В настоящем параграфе будут рассмотрены схемы наиболее распространенных типов логических ИС. Транзисторно-транзисторные логические схемы (ТТЛ) состоят из цепи И, построенной на основе многоэмиттерного транзистора, и транзисторного инвертора. На рис. 10-1, а показана принципиальная схема трехвходо-вого типового логического элемента транзисторно-транзисторной серии К155. Многоэмиттерный транзистор в схеме рис. 10-1, а образует трехвходовую цепь И. В случае присоединения хотя бы одного эмиттера этого транзистора к потенциалу, близкому к нулю, транзистор насыщается и тем самым присоединяет к нулевому потенциалу вход инвертора, состоящего из трех одно-эмиттерных транзисторов. Если же на все входы (эмиттеры) а)5)в) 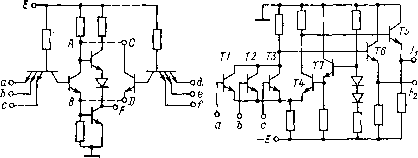 Рис. 10-1. Примеры схем логических ИС типов ТТЛ (а и б) и ТЛЭС (в) цепи И подан потенциал, близкий к напряжению питания (потенциал «1»), то базо-коллекторный переход многоэмиттерного транзистора окажется смещенным в прямом направлении. Этот переход открывается, и ток из базовой цепи транзистора поступает на вход инвертора. Дополнительные выводы от точек А я В инвертора (рис. 10-1, а) позволяют реализовать схему И — ИЛИ —НЕ путем присоединения к этим точкам выводов С я D логического расширителя (рис. 10-1,6). Учитывая обозначения, приведенные на рис. 10-1, можно записать функцию, реализуемую логическим элементом рис. 10-1, а, в виде F = abc, а реализуемую логическим элементом по схеме рис. 10-1, а и б — в виде F = abc+def. Наряду с обычными схемами ТТЛ существуют схемы ТТЛ, в которых базо-коллекторные переходы ряда транзисторов шунтированы диодами Шоттки. Это позволяет существенно повысить быстродействие логических элементов. Транзисторные логические схемы с эмиттерными связями (ТЛЭС) отличаются тем, что открытые транзисторы в них не входят в режим насыщения. Благодаря этому повышается бы- 0 ... 58 59 60 61 62 63 64 ... 82 |












