Раздел: Документация
0 ... 84 85 86 87 88 89 90 ... 365 Перед нахождением корней полезно построить график функции, входящей в левую часть уравнения. Для получения графика можно прибегнуть к plot, но все равно понадобится запрограммировать функцию, поэтому имеет смысл воспользоваться fplot, которая к тому же позволяет получить более точный график по сравнению с plot (написанию собственных файл-функций посвящен разд. "Файл-функции" главы 5). В листинге 6.1 приведен текст требуемой файл-функции. Листинг 6.1. Файл-функция, вычисляющая левую часть уравнения function у = myf(х) у = sin(x) - x.A2.*cos(x); Теперь постройте график функции myf, используя fplot, и нанесите сетку. » fplottmyf, [-5 5]) » grid on Из графика функции, изображенного на рис. 6.1 (пояснения на графике нанесены средствами MATLAB), видно, что на этом отрезке имеются четыре корня. Один корень равен нулю, в чем несложно убедиться, подставив х = О в уравнение (6.1). 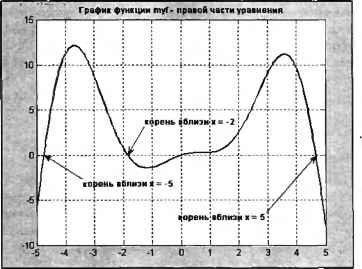 Рис. 6.1. График левой части уравнения (6.1) Уточните значение корня, расположенного вблизи х=—5, при помощи fzero: » xl = fzero(myf, -5) Zero found in the interval: [-4.7172, -5.2]. xl - -4.7566 Итак, приближенное значение корня равно -4.7566. При указании начального приближения к корню алгоритм fzero автоматически отделяет корень, т. е. вблизи заданного начального приближения находится отрезок, содержащий корень. В этом случае fzero может использовать больший интервал определения функции, чем исходный отрезок [-5, 5]. Проверьте ответ, вычислив значение функции myf в точке xl » myf(xl) ans = 2.6645e-015 Конечно, то, что значение функции близко к нулю, вообще говоря, не означает достаточную точность найденного корня. Гарантированная точность приближенного значения определяется расстоянием до его истинного значения или (что фактически то же самое) количеством верных значащих цифр. Заданию точности вычислений посвящен разд. "Управление ходом вычислений" данной главы. Для того чтобы увидеть больше значащих цифр корня xl, следует установить формат long и вывести xl еще раз (точность проводимых пакетом MATLAB расчетов не зависит от формата вывода результата!). » format long » xl xl = -4.75655940570290 Возникает вопрос, сколько в ответе точных значащих цифр, т. е. с какой точностью найдено решение. На компьютере вычисления производятся с числами, имеющими 52 двоичных разряда в мантиссе (без учета порядка числа). Это соответствует относительной погрешности представления чисел, которую возвращает функция eps, вызываемая без входных аргументов: » eps ans = 2 .220446049250313е-016 Алгоритм функции f zero по умолчанию находит корень уравнения с точностью eps, т. е. ± 2 в шестнадцатом знаке после десятичной точки — практически с максимально возможной точностью. Чтобы убедиться в этом, измените формат представления данных на long е и выведете xi: » format long е » xl xl = -4.756559405702904e+QQ0 Число значащих цифр увеличилось на одну (по сравнению с форматом long). Это самое точное представление числа в десятичной форме для пакета MATLAB. Измените последнюю цифру 4 на 5 и вычислите значение myf в точке xi: » xl = -4.75б559405702905е+000; » myf(xl) ans — -1.765254609153999e-014 Поскольку исследуемая функция сменила знак, то между этими значениями лежит искомый корень уравнения. Следовательно, ошибка в найденном корне в последней значащей цифре. Примечание Численное решение любой задачи требует дополнительных расчетов, подтверждающих (как правило, только косвенно) правильность полученных результатов. Для задачи нахождения корня уравнения вы только что проделали такой численный эксперимент. Проверьте работу fzero, вычислив корень myf, расположенный вблизи нуля, там, где точное значение корня равно нулю. >> х4 = fzero{myf, -0.1) Zero found in the interval: [0.028, -0.19051]. x4 - -1.242386505963434e-022 Функция f zero действительно гарантирует, что точность решения не меньше eps. Найдите самостоятельно корни х2 и х3, расположенные около точек -2 и -5. 0 ... 84 85 86 87 88 89 90 ... 365 |












