Раздел: Документация
0 ... 86 87 88 89 90 91 92 ... 365 Известно, что число всех корней полинома совпадает с его степенью. Убедитесь в правильности работы roots, вычислив значение полинома от вектора его корней: » polyval(р, г> ans 1.0е-012 * -0.1008 + 0.0899i -0.1008 - 0.08991 -0.0666 0.0027 - 0.0018i 0.0027 + O.OOIBi 0.0102 - 0.0053i 0.0102 + 0.0053i В верхней строке результата содержится общий множитель 1.0е-012, на который следует умножить каждую компоненту получившегося вектора. Нахождение экстремумов функций Вычислительные функции MATLAB позволяют найти точки минимума функции одной или нескольких переменных. Результатом является локальный минимум, т. е. точка, в окрестности которой значения исследуемой функции превышают ее значение в точке локального минимума. Для определения точек локального максимума нет специальной функции, поскольку достаточно искать минимум функции с обратным знаком. Минимизация функции одной переменной Поиск локального минимума функции одной переменной на некотором отрезке осуществляется при помощи fminbnd, использование которой схоже с fzero. Найдите локальные минимумы функции eAJ+sin37Tjt(6.2) на отрезке [—1.5,1.5]. Требуется предварительно создать соответствующую файл-функцию, назвав ее, к примеру ftest, или ввести inline или анонимную функцию (написанию собственных файл-функций посвящен разд. "Файл-функции" главы 5). Перед нахождением локальных минимумов постройте график исследуемой функции командой fplot. Из графика, приведенного на рис. 6.2, видно, что исследуемая функция имеет четыре локальных минимума. Вычислите значение х, при котором достигается второй локальный минимум, задав первым аргументом fminbnd имя файл-функции или указатель на нее, а вторым и третьим — границы отрезка, на котором ищется локальный минимум (установка точности и дополнительных параметров минимизации описана в разд. "Управление ходам вычислений" данной главы): » х2 = fminbndOftest, -0.5, 0) х2 = -0.1629 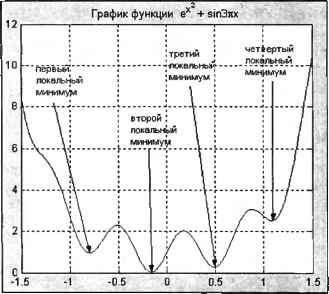 Рис. 6.2. Расположение локальных минимумов функции (6.2) Для лучшего понимания работы fminbnd задайте интервал поиска, содержащий все точки локальных минимумов. » хх = fminbnd(ftest, -1.5, 1.5) XX = 0.4861 Для одновременного вычисления значения функции в точке минимума следует вызвать fminbnd с двумя аргументами: » [х2, f] = fminbnd(@ftest, -0.5, 0) x2 = -0.1629 f = 0.0275 Так же, как и fzero, функция fminbnd может быть вызвана с тремя выходными аргументами: » [х2, f, flag] = fminbnd(@ftest, -0.5, 0); Аргумент flag может принимать три значения: положительное — при нахождении локального минимума, нулевое — при достижении максимального количества вызовов исследуемой функции и отрицательное — в случае расходимости вычислительного процесса. Найдите самостоятельно остальные локальные минимумы и максимумы функции (6.2). Рекурсивный алгоритм для поиска всех локальных минимумов на отрезке приведен в главе 8. Искать минимум функции можно также с применением fminsearch, рассматриваемой далее, которая предназначена для минимизации функции одной и нескольких переменных. Минимизация функции нескольких переменных Минимизация функции нескольких переменных является более сложной задачей по сравнению с минимизацией функции одной переменной, однако комбинированный адаптивный алгоритм функции fminsearch позволяет во многих случаях успешно решить эту задачу. Функция fminsearch требует указания начального приближения для искомой точки минимума, которое в случае функции одной переменной должно быть числом, а для функции нескольких переменных — вектором. Задайте начальное приближение равное -0.5 в примере предыдущего раздела и найдите точку локального минимума: » х2 = fminsearch(6ftest, -0.5} х2 = -0.1629 Выбирая последовательно подходящие начальные приближения, найдите все точки минимумов и максимумов функции. Рассмотрим теперь минимизацию функций нескольких переменных на примере функции двух переменных f(x, y) = sin7Lv-sin7iy.(6.3) 0 ... 86 87 88 89 90 91 92 ... 365
|
