Раздел: Документация
0 ... 87 88 89 90 91 92 93 ... 365 Сначала получите представление о поведении функции, построив ее линии уровня при помощи следующих команд (отображение линий уровня функции двух переменных описано в разд. "Контурные графики" главы 3): » [X, y] = meshgrid(0:0.01:2) ; » Z = sin(pi*X).*sin(pi*Y); » [CMatr, h] = contour(X, У, Z,[-0.96, -0.9, -0.8, -0.5, -0.1, 0.1, 0.5, 0.8, 0.9, 0.961); » clabel(CMatr,h) » colormap(gray) На получившемся графике, приведенном на рис. 6.3, видно расположение токальных минимумов и максимумов. Линии уровня функции sin их sin «у Локальные максимумы 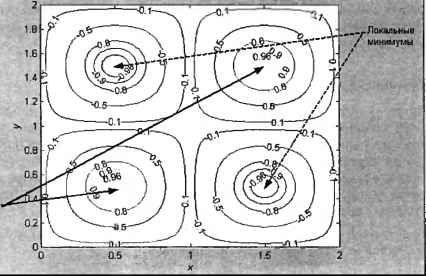 Рис. 6.3. Расположение локальных максимумов и минимумов функции (6.3) Перед применением fminsearch необходимо создать файл-функцию, вычисляющую значения искомой функции, причем аргументом файл-функции должен быть вектор, первый элемент которого соответствует переменной х, а второй — у. Текст требуемой файл-функции ftest2 приведен в листинге 6.2. Листинг 6.2. Файл-функция ftest2 function f = ftest2(v) x = v(l) ,-У = v[2) ; f = sin(pi*x) . *sin(pi*y) ; Теперь для нахождения локального минимума вызовите fminsearch с двумя входными аргументами— именем файл-функции и начальным приближением и выходным аргументом — вектором с координатами искомой точки минимума: »М = fminsearch(ftest2•, [1.4, 0.6]) м = 1.5000 0.5000 Решение найдено с точностью 1(И, как по значениям к и у, так и по значению функции. Для получения не только вектора с координатами точки минимума, но и значения функции следует вызвать fminsearch с двумя выходными аргументами: » [М, f] = fminsearch(@ftest2, [1.4, 0.6]) М = 1.5000 0.5000 f = -1.0000 Обращение к fminsearch с третьим дополнительным выходным аргументом flag » [М, f, flag] = fminsearch(@ftest2, [1.4, 0.6]); позволяет записать в него информацию о причине останова вычислительного алгоритма. Смысл его значений тот же, что и для функции fminbnd, рассмотренной в предыдущем разделе. Исследуемая функция может зависеть от произвольного числа переменных п. В этом случае входной аргумент argvect соответствующей файл-функции и начальное приближение должны быть векторами длины и. В нашей задаче не обязательно было программировать файл-функцию в М-файле. Поскольку входным аргументом анонимной функции может быть вектор, то следующие команды приведут к поиску минимума: » fun = @(v)sin(pi*v(l)).*sin(pi*v(2)); » [М, f] = fminsearch(fun, [1.4, 0.6]) м = 1.5000 0.5000 f = -1.0000 Примечание Optimization Toolbox, которому посвящена глава 16, содержит дополнительные средства минимизации функций. Например, fminunc можно использовать для поиска минимума функции нескольких переменных. Управление ходом вычислений Функции fzero, fminbnd и fminsearch допускают определение дополнительных параметров для управления вычислительным процессом и контроля за ним. Параметры задаются в управляющей структуре, которую мы будем называть options, как в справочной системе MATLAB, хотя имя может быть произвольным. Перед вызовом вычислительных функций следует предварительно сформировать переменную options в соответствии с характером требуемого контроля, воспользовавшись функцией optimset. Переменная options на самом деле является структурой. Это новый тип данных— до сих пор вы имели дело только с числовыми массивами. При чтении разделов этой главы умение работать со структурами не требуется, можно просто следовать приведенным правилам заполнения, просмотра и использования управляющей структуры options (работа со структурами данных описана в главе 8). Приступим к формированию структуры options на примере минимизации функции одной переменной (6.2) при помощи fminbnd. Получим сначала информацию о работе алгоритма минимизации на его последнем шаге. Для этого вызовем функцию optimset с одним выходным аргументом options и двумя входными Display и final, а затем укажем options в дополнительном четвертом входном аргументе fminbnd. Всюду дальше мы будем использовать термины свойство, вид контроля, опция или параметр (в данном случае Display) и значение свойства или параметра (в данном случае final). Установите формат вывода long, поскольку нам понадобятся все значащие цифры для анализа результата. » format long » options = optimset(Display, final); » x2 ~ fminbnd(@ftest, -0.5, 0, options) Optimization terminated successfully: 0 ... 87 88 89 90 91 92 93 ... 365 |












