Раздел: Документация
0 ... 45 46 47 48 49 50 51 ... 177 ки конь пи начал движение, у него будет множество возможностей обойти всю доску, побывав в каждой клетке только один pas. Мы решим задачу Эйлера двумя способами: прямым перебором и используя правило Вансдорфа. Однако, прежде чем мы приступим к реализации алгоритмов, необходимо провести небольшую подготовительную работу. В первую очередь нужно решить, как мы будем описывать шахматную доску. Очевидно, что ей нужно Поставить в соответствие матрицу. Каждый элемент этой матрицы будет описывать клетку доски. Однако адресоваться элементы будут, естественна, иначе, чем клетки. Если в случае реальной доски столбцы адресуются буквами от а до h, а строки — числами от 1 до 8, причем отсчет начинается с нижнего левого утла, то в случае матрицы ячейки будут адресоваться индексами от 0 до 7, а отсчет начнется с верхнеголевого угла. Это означает, что, например, клетке аЗ будет соответствовать элемент матрицы с индексами i-5, j-0. На то, что конь уже побывал в данной клетке, будет указывать значение соответствующего элемента описывающей доску матрицы: это номер хода, на котором конь находился в клетке. Если же конь еще ни разу не был в клетке, значением элемента будет нуль. Поэтому изначально в матрице доски должны быть одни нули. Создадим функцию, которая будет.формировать подобные матрицы для досок произвольных размеров: cb.esB fietd(n) := for i e 0.. а - 1 for j € 0., n - 1 field chess field(5) = field Го 0 0 0 o> 0 0 0 o) Далее нужно придумать, как можно представить в форме, понятной языку программирования, правила, по которым ходит конь, В общем случае имеется восемь вариантов хода (рис. 4.6). 0 1 2 3 4 5 6 ГЫтгтьп КПЗ тел Во всех вариантах хода есть одно общее: конь смешается на две клетки по одному измерен и ю н на одну клетку по другому. В зависимости от направления движения смещение будет иметь знак <+* или «-». Таким образом, каждый возможный ход можно описать нарой чисел, показывающей, на сколько клеток переместится конь по горизонтали и вертикали. Чтобы узнать, в какой клетке окажете» конь, сделав ход, нужно к индексам клетки, в которой он находится в данный момент, прибавить соответствующие числа из описывающей ход лары. Сами же пары удобно занести в векторы, которые в свою очередь являются элементами вектора: Как бы мы решали на бумаге задачу Эйлера о коне, не зная никаких специальных правил и методик? Почти наверняка мы использовали бы метод перебора с возвратом (именно его применял Эйлер). Суть этого метода заключается в следующей последовательности действий. I. Организуется иерархия шагов коня. Каждому варианту шага присваивается свой 2.То, куда будет сделан ход, зависит от того, какие варианты шага приведут коня в «пустую» клетку-, Если все варианты возможны, используется шаг с наименьшим индексом. Вели сделать этот шаг нельзя, осуществляется попытка сделать шаг с индексом, на единицу большим, — и так до тех пор, пока свободная клетка не будет найдена. 3.Если в результате очередного ujara конь попал в клетку, из которой невозможно сделать шаг в клетку, в которой он не был ранее, маршрут признается тупиковым. При этом конь должен сделать один шаг назад и «иогфооовать* походить в другую клетку (последовательно используя варианты шага, расположенные в иерархии позже тупикового). Если это невозможно, делается еще один шаг возврата и попытка осуществляется снова - и так до тех пор, пока «пустая* клетка не будет найдена, 4.Если решение найдено не будет, то конь вернется в исходную клетку, опробовав все возможные маршруты. О том же, что искомый маршрут обнаружен, можно судить по тому, что на поле не останется ни одной непосещенной клетки. Визуально алгоритм перебора с возвратом можно представить как последовательный обход графа (дерева) неизвестной структуры в поисках ветви максимальной длины. Пример подобного обхода для небольшого графа показан на рис. 4.7. Чтобы найти наиболее длинную ветвь из шести узлов, понадобилось сделать 17 шагов. В случае графа, соответствующего обходу конем шахматной доски, чтобы найти ветвь из 64 узлов, мо-жег понадобиться сделать миллионы или даже миллиарды шагов. Каждый из возможных маршрутов коня может быть визуализирован как ветвь графа. Клеткам маршрута будут соответствовать узлы. Так как любой маршрут будет иметь часть, общую с. другими маршрутами, ветви при движении сверху вниз сливаются, сходясь к одному узлу, соответствующему клетке начала движения. Чтобы найти ветвь графа требуемой длины, нужно организовать последовательный обход его ветвей слева направо или справа налево (см. рис. 4.7). Наиболее простой способ это сделать с помощью средств программирования связан с использованием рекурсии. индекс. 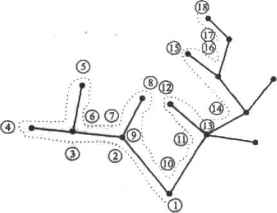 Рис. 4.7. Обход графа посредством последовательного перебора с возвратом Алгоритм рекурсивно вызываемой функции, выполняющей обход графа маршрутов, будет несложен. Каждая ее активация будет соответствовать отдельному узлу графа. Основная цель активации — выполнить очередной шаг вверх к следующему узлу ветви. Для этого посредством цикла проверяется, имеется ли вариант хода, который приведет коня в нетюсещеннуто ранее клетку. Если такой обнаруживается, осуществляется рекурсивный вызов, создающий соответствующую этой клетке активацию. Текущая же активация ожидает результата дальнейшего исследования ветви, который будет возвращен в конце концов новой активацией. Если, просмотрев все варианты хода, код активации обнаружит, что возникла тупиковая ситуация, активация должна быть разрушена, а в точку соответствующего eft вызова, относящегося к г[редыдутцей активации, должно быть возвращено информационное сообщение об этом. Получив это сообщение, нижележащая активация проверит, можно ли посредством хода с более низким приоритетом, чем осуществленный ранее, перейти в «пустую» клетку. Если такой вариант хода имеется, действия повторятся. Если же все варианты уже исчерпаны, активация разрушится, передав сообщение о тупике нижележащей активации. И так до тех пор, пока не будет найден нужный маршрут. Об успехе будет говорить то, что очередная активация окажется в стеке в качестве элемента под номером п!, где п — размерность доски. При этом активация должна быть разрушена, а в точку вызова возвращено сообщение, говорящее об успешном завершении обхода. Данное сообщение должно передаваться сверху вниз от активации к активации, разрушая их. В качестве такого сообщения имеет смысл использовать матрицу с найденным маршрутом. Приведенное выше описание алгоритма, который нам предстоит реализовать, скорее всего, покажется вам запутанным и малопонятным. Это неудивительно ввиду чрезвычайной абстрактности рекурсивных алгоритмов. Вернитесь к описанию алгоритма обхода после того, как мы создадим соответствующую ему функцию. При атом вы легко поймете то, что трудно понять сейчас Функцию, предназначенную для рекурсивного обхода графа маршрутов коня, мы назовем brain. Она будет принимать четыре параметра: индексы клетки, из которой должен быть сделан ход (i и j), матрицу с информацией о том, в каких клетках конь уже побывал (field), количество «заполненных* на момент вызова клеток (п). Чтобы запустить работу алгоритма, активировав brain, необходимо предварительно создать описывающую доску матрицу нужной размерности посредством функции chessfield, а затем заменить 0 ... 45 46 47 48 49 50 51 ... 177 |












