Раздел: Документация
0 ... 16 17 18 19 20 21 22 ... 36 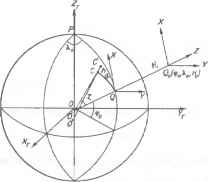 Рис. 8.1. Топоцентрическая горизонтная в сфероидическая (сферическая) полярные системы координат. В произвольной точке Q{%,\) эллипсоида проведем нормаль QO к этой поверхности (рис. 8.1.), через которую можно провести бесчисленное множество нормальных сечений. Из них мы выберем два главных: сечение, совпадающее с плоскостью меридиана PQP, называемое меридианным, и сечение, ортогональное первому в точке Q, называемое сечением первого щих изменения начала координат и азимута в начальном (исходном) пункте, и второго рода (dBi dL2). учитывающих изменения сжатия и большой полуоси исходного и нового эллипсоидов. В настоящее время разработаны и используются алгоритмы таких преобразований с промежуточным переходом в геоцентрические координаты. 8.2. ОБЩАЯ ТЕОРИЯ КАРТОГРАФИЧЕСКИХ ПРОЕКЦИЙ. Включает совокупность теоретических положений, являющихся основой получения и использования всего множества картографических проекций. 8.2.1. Системы координат принятые в ГИС В теории и практике ГИС применяются пространственные прямоугольные, криволинейные, плоские прямоугольные и полярные системы координат. стей принимают поверхности шара, эллипсоида вращения, и в отдельных случаях — трехосного эллипсоида. К элементам геодезической основы относят опорные пункты, определённые в системе геодезических координат, принятой в данном государстве, и координатные сетки, связанные с этими опорными пунктами. Геодезические системы координат включают: параметры референц-эллипсоида (величина большой полуоси а или малой Ь, сжатие а или эксцентриситет е); высоту геоида над референц-эллипсоидом в начальном пункте; исходные геодезические даты (геодезические широта и долгота начального пункта, азимут на ориентирный пункт). В работах по геодезии, топографии и картографии, выполняемых в России, используется эллипсоид Красовского (й=6378245м; а=1/298.3), начальный пункт Пулково; превышение геоида над референц-эллипсоидом в начальном пункте равно нулю. Принята Балтийская система высот. Счёт высот в этой системе ведётся от нуля Кронштатского футштока. В процессе выполнения картосоставитель-ских работ определяют геодезическую систему координат и систему высот, которые были приняты при создании исходного картографического материала. Это выявляется по формулярам листов карт или по литературно-описательным источникам. В случаях когда геодезическая основа исходного материала, используемого для создания карт, имеет другую геодезическую систему координат, необходимо осуществить преобразование этой системы в геодезическую систему координат, принятую в данном государстве. Эта задача, как правило, решается аналитически — путем введения так называемых дифференциальных поправок первого и второго рода. Во многих книгах по высшей и сфероидической геодезии даны формулы для определения дифференциальных поправок первого рода (dBi dL )s учитываю- вертикала. С учётом этого определяют и используют различные системы координат: геодезическую, геоцентрическую, топоцентрическую, сфероиди-ческую (сферическую), изометрическую и локальные системы. В геодезической системе определяются геодезическая широта точки <р -угол между нормалью QO к поверхности эллипсоида в данной точке эллипсоида Q и плоскостью экватора и долгота этой точки Я - двухгранный угол между плоскостями начального меридиана и меридиана данной точки. В пространственной геоцентрической системе координат OXYJZt начало совмещено с центром масс Земли (с центром эллипсоида вращения), ось Z -направлена на средний северный полюс Земли, ось Хт - в точку пересечения Гринвичского меридиана с экватором, ось К - на восток Связь геоцентрической и геодезической системы координат выражается формулами: Хг = N cos <р cos Я; Yr = N cos <р sin Я; Zr = #(l-e2)sin$j, где N = aj{\ — е2 sin2 <р2 — радиус кривизны сечения первого вертикала в данной точке а, е2 - соответственно большая полуось эллипсоида вращения и квадрат первого его эксцентриситета. Топоцентрической горизонтной системой координат (рис. 8.1.) будем называть систему, в которой начало совмещено с произвольной точкой пространства Q„ ((р„квНХ ось Ллежит в плоскости меридиана точки Q и направлена на северный (средний) полюс, ось Z совпадает с нормалью OQ0 к поверхности эллипсоида в точке Q, ось Y- дополняет систему до левой. Формулы связи топоцентрической и геодезической систем координат имеют вид: X = (N + A)[sin (р cos <р0 - cos (р sin <рй соЯ - Я0)] + + е2(лг0 sin>0 - Nsincos,,; Y = {N +h)cos<psm(A, — Я0); Z = (N + A)[sin (p sin <pB + costpcos(p0 соЯ - Я0 )j + +e2 (NB sin tp0 - N sin tp)sin <рй - (N0 + H0), где <p, Я; (p0, Я0 - соответственно географические координаты в текущих точках и точке полюса; Н0 — высота точки полюса относительно поверхности эллипсоида; h — превышения точек. В сфероидической полярной системе координат z=const, a=const а - углы между нормальными плоскостями в точке полюса Q, z — углы между нормалью OQ0 и направлениями в точке О на текущие точки С, лежащие в соответствующих нормальных плоскостях; h - превышения точек поверхности Земли (при отображении поверхности эллипсоида все h=0). С точностью до членов с е4 получаем формулы связи полярных сферои-дических и геодезических систем координат sinzcosa = f, +е2г[г, sin>- cos>0]+...; sin z sin a = cos>sin - Я0); cosz = f3 + e2 r[f3 sin <p- sin <p0 ]+...; где f, = sin>cosp0 -cos>sin>0 сов(Я- Я0) f3 = sm(ps\n(pB + coscosfj0 соЛ — Я0) т = sin7 -sin#>0 Изометрическую систему координат определяют под условием, чтобы при равенстве дифференциалов изометрических широт и долгот dq и dX соответствующие им бесконечно-малые дуги меридианов dat, и параллелей Ат2 8.2.3. Бесконечно малая сфероиднческая трапеция и ее изображение на плоскости Элементами бесконечно малой сфероидической трапеции являются (рис. 8.2): dsl = Md<p — бесконечно малый отрезок меридиана; <Ьг = rdX — бесконечно малый отрезок параллели; \Уг 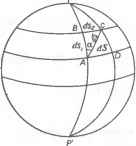 ds = [ds] +ds] 2 — линейный элемент эллип- соида; Рис. 8.2. Элементы сфероидиче- а = aTCJ ской трапеции Mdw) линейного элемен- та; dS = dslds1 = Mrd<pdX - площадь бесконечно малой трапеции, где М = a(l-e2)/(l-e2sin2i75) - радиус кривизны меридианного сечения; г - N cos i75 - радиус кривизны параллели. Элементами изображения бесконечно малой сфероидической трапеции на плоскости являются (рис. 8.3): пиний устанавливается в зависимости от назначения карты. Вид картографической сетки зависит от уравнений данной проекции. были также равны, что имеет важное значение при разработке и использовании ряда картографических проекций (равноугольных). Формула изометрической широты точек эллипсоида вращения имеет вид: <7 = 1пГ; V = tg(45 + <p/2)/tg (45° + у/ll), у/ = arcsin(esint7?). Локальные системы координат функционально связаны с прямоугольной системой координат создаваемой карты (модели ГИС) и предназначены для решения трёх основных задач: ввода в память ЭВМ изображения с исходных картографических материалов; построения системы условных знаков и непосредственного математического описания исследуемых кривых; устранения (ослабления) искажений из-за деформации бумаги, не совмещения красок при печати, ошибок составления и.т.п. 8.2.2. Определения картографических проекций, картографические сети Дадим два определения проекции: 1.Картографической проекцией называется математически выраженный способ отображения поверхности Земли или других небесных тел, принимаемых за эллипсоид, сферу или иные регулярные поверхности, на плоскости. 2.Картографической проекцией называется способ установления взаимно-однозначного соответствия точек отображаемой поверхности и плоскости. Изображение на картах линий меридианов и параллелей в принятой картографической проекции называется картографической сеткой. Частота её 0 ... 16 17 18 19 20 21 22 ... 36 |












