Раздел: Документация
0 ... 17 18 19 20 21 22 23 ... 36 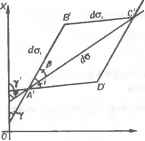 da = edq)1 + 2fd<pdX + gdZ2 ] - линейный элемент на плоскости; dax -- 4ed<p — изображение на плоскости бесконечно малого отрезка меридиана; da2 = yfgdA — изображение на плоскости Y бесконечно малого отрезка параллели; Рис.8.3. Элементы изображения бесконечно малой сфероидической трапеции £ = 1-90° =arctg(-£) i = arctg— — угол между изображениями меридианов и параллелей в точках проекции; отклонение угла i от прямого; /?=arcct-—ctg h М е г азимут линейного элемента на проекции; dL = da,da2 sim" = hd<pdX - площадь изображения бесконечно малой трапеции на проекции. Здесь: e,f, g— коэффициенты Гаусса: e = xl + yl;f = x9xA+y9yA; 8 = *\ +у\\ h = x ух-хлу . 8.2.4. Масштабы В теории картографических проекций рассматриваются понятия и формулы линейных масштабов и масштабов площадей. Линейные масштабы подразделяются на главный (общий см п. 8.2.10.) и частные масштабы длин. Частным масштабом длин отображения в данной точке по данному направлению называется отношение бесконечно малого отрезка на проекции к соответствующему бесконечно малому отрезку на поверхности эллипсоида (сферы). Формула частных масштабов длин в каждой точке проекции по заданному направлению а имеет вид. p.2 = т1 cos2 а + /wjcosjsin2a + /и2 sin2 а. При азимутах направления соответственно а = 0 и а = 90° получаем т = — \х2 +y2jfr — формула частного масштаба длин вдоль меридиа- нов; п = -[х2 + у2]2 - формула частных масштабов длин вдоль параллелей; хр> У9\ хл> У л ~ частные или обыкновенные производные прямоугольных координат проекции по широте <р и долготе А. Частным масштабом площади называют отношение бесконечно-малой площадки d£ на проекции к соответствующей бесконечно-малой площадке на поверхности эллипсоида (сферы) dS. Формулы частных масштабов площадей р имеет вид hи р =-= тп cose = ab, F Mr где e = arctg- ~j - отклонение угла i между изображениями меридианов и параллелей на проекции от прямого; / = *«Л + У „Ул i h = хгУх ~ хлУг В каждой точке по двум ортогональным направлениям частные масштабы длин принимают экстремальные значения: а - наибольший, Ь - наименьший частные масштабы. Направления, по которым частные масштабы экстремальны называются главными. В проекциях с ортогональной картографической сеткой главные направления совпадают с направлениями меридианов и параллелей. Экстремальные частные масштабы длин определяются по формулам
У Рис. 8.4. Бесконечно малыеРис. 8.5. Схема построения эллипса окружность и трапецияискажений на эллипсоиде В общем случае бесконечно малая окружность на поверхности эллипсоида (сферы) изображается на плоскости бесконечно малым эллипсом. В частных случаях, а именно в равноугольных (конформных) и полуконформных проекциях, в которых частные масштабы длин вдоль меридианов и параллелей равны (т=п), бесконечно малая окружность на поверхности эллипсоида (сферы) изображается на плоскости подобной бесконечно малой окружно- 8.2.6. Искажения картографических проекций Важнейшим фактором выбора и использования картографических проекций являются величины и характер искажений используемых проекций. Их анализ позволяет оценить достоинства рассматриваемых проекций и использовать полученные данные для решения ряда практических и научных задач. Обычно отмечается, что на картах имеют место два вида искажений: искажения длин во всех проекциях; углов и площадей - во всех проекциях, кроме соответственно равноугольных и равновеликих проекций, возникающие из-за изменений частных масштабов в точках проекций и дающие характеристику отображений в этих точках; искажения в длинах конечных прямолинейных отрезков и углах между ними, а также в азимутах этих направлений, возникающие при выполнении измерений на картах из-за кривизны изображения геодезических линий. Геометрическую интерпретацию искажения даёт понятие об эллипсе искажения (см. рис. 8.4, 8.5). А + В , А-В а = —-—; о = —-—, 22 где Л=т2 +и2 +2mncose); В = m2 + п - Imncos1. 8.2.5. Условия отображения поверхности эллипсоида (сферы) иа плоскости Картографические проекции могут быть равноугольными, равновеликими и произвольными (в частных случаях равнопромежуточными) по характеру искажений. При получении этих проекций необходимо добиться, чтобы их уравнения удовлетворяли соответствующим условиям отображения. Равноугольными проекциями называют такие, в которых отсутствуют искажения углов и азимутов линейных элементов, т.е. в которых одновременно выполняется два условия: картографические сетки этих проекций должны быть ортогональны и в каждой точке проекции, частные масштабы длин не должны зависеть от направлений, по которым они определяются. Эти условия принимают вид т = п; f = О Тт или хл =--у • ул = —х (условие Коши-Римана) ММ Равновеликими проекциями называются такие, в которых площади S и I указанных областей на поверхности эллипсоида (сферы) и на плоскости тождественно равны (пропорциональны). В этих проекциях должно быть р=1; или h= Mr; или mncose = ab = 1 Равнопромежуточными называются проекции, сохраняющие длины по одному из главных направлений. Наиболее часто к ним относят проекции с ортогональной картографической сеткой, в которых сохраняются длины либо вдоль меридианов, либо вдоль параллелей. £j(=i[(fl-l)2+(ft-l)2]; .;-£[(f-oWiy] критерии Эйри; "*2- 2 LV£ е\ к = — [in2 а + In2 б] - критерий Эйри-Каврайского; 1 2* е2, = — -1) da - критерий Иордана 2л о 1 1гг =— Fin2 fjda - критерий Иордана-Каврайского 2п о а - arctg {fib-1) — кРитерий Конусовой, при помощи которого оце- нивается или задается характер искажений проекций: а = 0 — для равноугольных проекций, 71 а ~~2 — Для равновеликих проекций, „ тс О < а — для проекции произвольных по характеру искажении. Кроме указанных, для оценки достоинств картографических проекций были также предложены и использовались другие критерии (Клингача, Ве-бера, Эйзенлора, Фролова и др.). Заметим, что для проекций с ортогональной картографической сеткой во всех указанных критериях экстремальные частные масштабы «с» и «Ь> принимают значения частных масштабов длин вдоль меридианов т и вдоль параллелей п. Величины искажений длин в пределах всей изображаемой области оцениваются при помощи критериев минимаксного или вариационного типов. Критерием минимаксного типа является критерий П.Л.Чебышева, согласно которому для исследуемой проекции определяется (в пределах всей изображаемой области) отношение наибольшего значения частного масштаба длин Мтах к наименьшему значению цтт- При использовании критериев вариа- стью. Отметим, что для геометрической интерпретации искажений удобнее использовать не бесконечно малые, а конечные величины. Исходя из этого, эллипсом искажений или индикатрисой (указательницей) Тиссо назвали эллипс конечных размеров (например, при радиусе окружности R=l), соответствующий полученному на плоскости бесконечно малому эллипсу. Если по рис. 8.4, 8.5 определить углы и и v между главными направлениями и направлениями на текущие точки на эллипсоиде и плоскости и обозначить через у наибольшую их разность — = и0 - vc , то наибольшие искажения углов проекции определяются формулами: w а-Ь w 2-Ja-b w a — b sin— =--; cos— =-—; /в— = —p= 2 a+b 2 a + b 62 2-Jal) где a, b — экстремальные частные масштаба длин Искажения длин на проекции характеризуются тремя показателями • Различают относительные искажения длин в данной точке проекции по данному направлению, относительные искажения длин в данной точке по всем направлениям и среднеквадратические (среднеарифметические) величины искажений в пределах всей изображаемой области. За меры относительных искажений длин в данной точке по данному направлению принимают следующие величины: 11, , ч v,= -l; v2=ln/y; v3=l--; vt=-[/j -1). Все эти величины различаются между собой лишь малыми второго или более высоких порядков малости относительно самих их величин. За общую меру относительных искажений длин в данной точке по всем направлениям принимают формулы, предложенные различными учеными и называемые критериями по их именам: 0 ... 17 18 19 20 21 22 23 ... 36 |












