Раздел: Документация
0 ... 20 21 22 23 24 25 26 ... 36 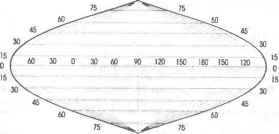 Рис.8.8. Равновеликая синусоидальная псевдоцилиндрическая проекция Сансона. Эти проекции могут быть только равновеликими или произвольными по характеру искажения и применяются, главным образом для картографирования всего земного шара в целом. 8.3.3. Конические проекции
Коническими называют картографические проекции, в которых параллели изображаются концентрическими окружностями, а меридианы - пучком прямых, проведенных из центра окружностей. При этом углы в точке полюса между меридианами на проекции и эллипсоиде Рис.8.9. Системы координат в нор- (сфере) пропорциональны и, следователь-мальной конической проекции но, на проекции в точке полюса возникает разрыв изображения (рис.8.9). Общие уравнения конических проекций и формулы частных масштабов длин вдоль меридианов (от) и параллелей (п), наибольших искажений углов (со) имеют вид х = рю - pcosS; у = psinS; P=f{<p\ 6=аХ\ секающие на поверхности эллипсоида все меридианы под постоянными углами), изображаются прямыми линиями, что существенно облегчает решение навигационных задач по этим картам. Цилиндрические проекции целесообразно применять для картографирования территорий, расположенных вблизи экватора, симметрично к нему и сильно вытянутых по долготе. 8.3.2. Псевдоцилиидрическне проекции Псевдоцилиндрическими называются проекции в которых параллели изображаются прямыми линиями, а меридианы - кривыми, симметричными относительно среднего прямолинейного меридиана (рис.8.8). Общие уравнения этих проекций, формулы частных масштабов длин вдоль меридианов (/и), параллелей (и), площадей (р), наибольших искажений углов (со) и отклонений углов между меридианами и параллелями на проекции от прямого е имеют вид: m = xvsece/M; n = ykjr\ tg*=-y„/v В псевдоцилиндрических проекциях можно изобразить всю картографируемую поверхность, а при необходимости повторить части изображения по долготе. Географические полюса можно показать точками или линиями, которые параллельны экватору и называются полярными линиями. Меридианы имеют заданный вид, изображаются чаще всего эллипсами или синусоидами, но можно получить псевдоцилиндрические проекции, в которых меридианы имеют вид парабол, гипербол и других кривых. М sin = \т - и/(»* + и). Проекции имеют два постоянных параметра а и Л. Они могут быть равноугольными (в них т = п), равновеликими (в них р=тп), равнопромежуточными (в них т = 1 или п = 1) и произвольными по характеру искажения. Их целесообразно использовать для картографирования территорий расположенных в средних широтах или в южных широтах, асимметричных к экватору и сильно вытянутых по долготе, например при создании многих карт России. 8.3.4. Азимутальные проекции 180 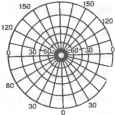 Азимутальными называют проекции, в которых параллели (альмукантараты) изображаются концентрическими окружностями, а меридианы (вертикалы) - прямыми линиями, пересекающими-ся в центре окружностей под углами, равными разностям долгот соответствующих меридианов (рис. 8.10). В азимутальных проекциях шара их общие уравнения и формулы частных масштабов длин вдоль меридианов (р1=т), параллелей (уц, =п) и наибольших искажений углов (а>) записываются с использованием полярных координат z, а в виде х = pcosa; у = psiner; р = /(z); H=pz/r /=p/sinz; siny = / -/Ц+ ,), где r - радиус земного шара. Рис.8.10. Нормальная азимутальная проекция Для получения азимутальных проекций эллипсоида в целях картографирования полярных областей используют конические проекции, в которых полагают, что постоянный параметр а = 1. Эти проекции могут быть равноугольными (в них р= р), равновеликими (в них р = рлр7), равнопромежуточными вдоль меридианов и параллелей (вертикалов и альмукантаров) (в них р\ =1 или =1), произвольными по характеру искажений. Их целесообразно использовать, как проекции эллипсоида, при картографировании полярных областей и, как проекции шара для картографирования других территорий, но имеющих округлые очертания. Из этих проекций, особое внимание заслуживает равноугольная азимутальная (стереографическая) проекция, которая является единственной проекцией в которой нет искажений форм конечных фигур. При картографировании других территорий, кроме полярных, в качестве азимутальных проекций эллипсоида используют равноугольную проекцию Лагранжа, в которой полагают, что постоянный параметр а = 1. 8.3.5. Перспективные азимутальные проекции Эти проекции подразделяют на проекции с «негативным» и «позитивным» изображениями. В первых проектирование отображаемой поверхности из точек пространства, называемых точками зрения, прямолинейными визирными лучами на картинную плоскость осуществляется со стороны вогнутости этой поверхности, во вторых - со стороны выпуклости отображаемой поверхности. К перспективным азимутальным проекциям с «негативным» изображением относятся: гномоническая проекция, в которой ортодромии, - линии кратчайших расстояний на поверхности сферы, изображаются прямыми (точка зрения находится в центре шара); 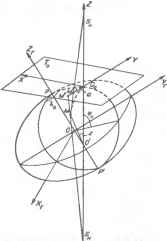 H[Dcos<p0 - R] D- R0 cos0>J Н Рис 8 11 Перспективно-азимутальные проекции прн отображении на горизонтальную картинную плоскость D— Rcostp И — высота фотографирования Прямоугольные координаты данной проекции на наклонную картинную плоскость (математической модели перспективного кадрового космического снимка) можно представить следующими формулами: а,Х + Ь,Г-с,Я a3X + b3Y-c3H а2Х + b2Y-c2H Уо~ аъХ + Ь-с3Н где /, х0, у0 - элементы внутреннего ориентирования снимка (f - фокусное расстояние, х0, у0 - прямоугольные координаты главной точки снимка), ci> *i> с, ~ направляющие косинусы, определяемые по значениям угловых элементов внешнего ориентирования снимка, вычисляемые в той или иной принятой системе этих элементов. Использование этих проекций позволяет дать математическое описание космических снимков, выполнить их преобразование для создания карт, решать по ним ряд задач. 8.3.6. Псевдоконические проекции Псевдоконическими называются проекции, в которых параллели представляют собой дуги концентрических окружностей, а меридианы - кривые, симметричные относительно среднего прямолинейного меридиана, на котором расположен центр параллелей (рис.8.12). стереографическая проекция, которая является равноугольной проекцией и единственной, в которой нет искажений форм конечных фигур (точки зрения располагаются на поверхности шара); ортографическая проекция, в которой нет искажений вдоль альмукантара-тов (точка зрения располагается в бесконечности и поэтому эту проекцию используют для создания некоторых карт небесных тел). Перспективные азимутальные проекции с «позитивным» изображением -являются математическими моделями кадровых космических снимков. Формулы прямоугольных координат этих проекций эллипсоида на горизонтальную картинную плоскость и частных масштабов длин проекций шара имеют вид: ВВ где A = (N + A)[sin0>cos(Po - cossin<o0cos(/ - )] + + e2(N0 sin$?0 - Nsin0>)cos0>„; Б = (N + /i)(cos0>sin(A - Ло)); B = (N + /i)[sinsin(P0 + costpcos<p0 cos(A - A)} + + e2(/V0siniT>0 - Ns\nip)sm<p0-(N0 + H), h - превышение точек местности над поверхностью эллипсоида. Формулы частных масштабов длин этих проекций шара принимают вид 0 ... 20 21 22 23 24 25 26 ... 36 |
||||||||||||||||||||












