Раздел: Документация
0 ... 21 22 23 24 25 26 27 ... 36 = i[(+)/p-f; 2 2 Из определения этих проекций следует, что в них картографические сетки неортогональны, а длины дуг меридианов являются функциями и широты, и долготы. 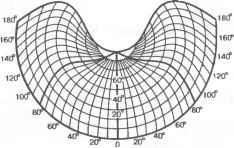 Рис. 8.12. Псевдоконическая проекция Следовательно, эти проекции не могут быть равноугольными и сохранять длины вдоль меридианов. Они могут быть только равновеликими (в них р = mncose = 1) и произвольными по характеру искажений. Из этих проекций наибольшее распространение (особенно во Франции и зависимых от нее странах) получила равновеликая псевдоконическая проекция Бонна. 8.3.7. Псевдоазимутальиые проекции Псевдоазимутальными называются проек- ции, в которых параллели изображаются концентрическими окружностями, а меридианы — кривыми или прямыми, сходящимися в центре параллелей. При этом меридианы с долготами 0°, 360° совпадают и изображаются либо прямыми (рис.8.13.), либо кривыми, в каждой 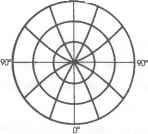 Рнс. 8.13. Нормальная псевдо- точке которых имеют одинаковую кривизну, азимутальная проекция Проекции применяются только в косой ориентировке для создания эффекта сферичности при рассматривании карт, созданных в этих проекциях. 8.3.8. Поликоиические проекции Поликоническими называются проекции, в которых параллели - дуги эксцентрических окружностей с центрами, расположенными на среднем прямолинейном меридиане, а меридианы — кривые, симметричные относительно среднего меридиана и экватора (рис. 8.14). Эти проекции могут быть равноугольными (в них т = п; £ = 0), равновеликими (в них р = mncos£ = 1) и произвольными по характеру искажений. Различают поликонические проекции в широком смысле, из которых наибольшее применение и значение имеет равноугольная проекция, в которой все меридианы и параллели изображаются окружностями 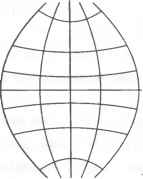 Рис. 8.14. Поликоннческая проекция (проекция Лагранжа). Уравнения этих проекций и формулы их характеристик можно представить в виде: х = рю - pcosS; у = psinS; p=/ii»; 8=/г{<р, я) /=рЧ5я> п=-ррА tg£ = (pSv)/pv; PvPSx m = —-sece; n = —-; mr В поликонических проекциях в узком смысле радиусы параллелей равны р - NcXgq> и частный масштаб длин вдоль среднего меридиана т0 = const, в частности m0 = I. Из этих проекций наибольшее распространение (особенно в США) получила простая поликоническая проекция для создания карт в широкой и узкой зонах, в которой дополнительно вводится условие, что частные масштабы длин вдоль параллелей п = 1. Для создания площадной авиационной карты масштаба 1:1 ООО ООО во многих странах используется видоизмененная простая поликоническая проекция. Эта проекция используется, как многогранная, каждый лист определяется в своем варианте проекции, все меридианы изображаются прямыми линиями, отсутствуют искажения длин на крайних параллелях и на меридианах, отстоящих от среднего на ДА = ±2°, средние параллели определяются пропорциональным делением по широте вдоль прямолинейных меридианов. 8.3.9. Проекции Гаусса-Крюгера и UTM Проекция Гаусса-Крюгера определяется для картографирования территорий в узкой зоне (для топографических карт) и в широкой зоне. В первом случае проекцию получают, исходя из трех условий: она симметрична относительно среднего меридиана и экватора, она равноугольна и в ней на среднем меридиане нет искажений длин. Проекции Гаусса-Крюгера в широкой зоне получают путем последовательного выполнения трех равноугольных отображений: вначале равноугольно отображают эллипсоид на поверхность шара по способу Мольвейде, затем определяют прямоугольные координаты проекции шара Гаусса-Ламберта и наконец отображают плоскость на плоскость под условием сохранения длин на среднем меридиане. Формулы прямоугольных координат, частных масштабов длин и сближения меридианов проекции Гаусса-Крюгера имеют вид: Я2 х = S + — N cos<psm<p+... Я3 у = ANcostp + —TVcos3[l + rf - tg2 #>]+...; Я2Я* m = l + —cos2 1 + 772) + —cos4 <p\b - 4tg2 <pj, Я3 у - Xsmtp + —cos2 0>sinl + З/72), где 5 - длина дуги меридиана от экватора до данной параллели; if =e2cos20>; е1 - квадрат второго эксцентриситета эллипсоида. Проекция UTM, нашедшая широкое распространение в странах НАТО, отличается от проекции Гаусса-Крюгера тем, что в ней на среднем меридиане частный масштаб длин т0 не равен единице, как в проекции Гаусса-Крюгера, а величине т0 = 0.9996. С учетом этого формулы связи этих проекций принимают вид: -при определении проекции UTM в левой системе прямоугольных координат хитм = кхгк* Уитм ~ кУгк титм = апгк Уитм ~У г к -при определении проекции UTM в правой системе прямоугольных координат хигм = кУгк Уитм =кхгк.< титм = гк > Уитм = У г.к где к = 0.9996 Нулевые изоколы в проекции UTM проходят примерно параллельно среднему меридиану при удалении от него в обе стороны около 200 км. 8.3.10. Проекция Чебышева. Состояние решения общей проблемы изыскания наилучших проекций. Приоритет в постановке и решении проблемы о наилучших картографических проекциях принадлежит российским ученым. В 1853 г. великий русский математик П.Л. Чебышев сформулировал теорему о наилучших равноугольных проекциях, согласно которой наилучшими из них являются проекции, в которых на контуре картографируемой территории натуральный логарифм частного масштаба длин имеет постоянное значение. Эту теорему в 1894 г. доказал Д.А. Граве. Определение этих проекций сводится к решению двух задач. Вначале на основе решения уравнения Лапласса при заданных граничных условиях определяются частные масштабы длин в точках области картографирования по их постоянным значениям на контуре территории. Затем, записав уравнения частных производных прямоугольных координат по широте и долготе с учетом полученных значений масштабов, определяют прямоугольные координаты проекции. В настоящее время разработан ряд способов вычисления проекции Чебы-шева, использование которой обеспечивает уменьшение искажений на картах до 4 раз по сравнению с другими равноугольными проекциями. В 1898 г. Н.Я. Цингер высказал гипотезу о получении наилучших равновеликих проекций. В 1933 г. В.В. Каврайский показал недостаточность этой гипотезы, но конкретных решений этой проблемы не дал. В 1968 г. Г.А. Мещеряков опубликовал монографию, в которой критиковал исследования Н.Я. Цингера и В.В. Каврайского, сформулировал и доказал теорему о получении наилучшей равновеликой проекции для картографирования территории полушарий. Но общего решения также не дал. Таким образом, проблема получения наилучших равновеликих и других по характеру - искажений проекции пока еще не решена. 9. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ СОЗДАНИЯ БАЗОВЫХ КАРТ И МЕТОДОВ РЕШЕНИЯ ПРОСТРАНСТВЕННЫХ ЗАДАЧ ГИС ПО КАРТАМ. ГИС является интегрированной информационной системой. Основная унифицированная форма информации в ГИС, с которой работает пользователь, - картографическая. Именно карты содержат обширную, разнообразную обобщенную информацию об объектах и явлениях реального мира, представленную в соответствующих системах координат. Карты обеспечивают возможность решать разнообразные задачи ГИС на основе использования отображенной на них пространственно локализованной информации. Следовательно, пользователь ГИС должен иметь достаточные знания: -о способах создания карт, их свойствах и особенностях, способах отображения на них элементов природы и общества; -уметь определять по картам картографическую информацию на основе использования существующих математических и других методов ее анализа и синтеза. Ниже рассматриваются основные положения создания и использования карт. 9.1. ЭТАПЫ И ОСНОВЫ СОЗДАНИЯ КАРТ Географические карты, в том числе базовые карты ГИС, создаются в четыре этапа, включающие: редакционно-подготовительные работы; создание составительских оригиналов; подготовку карт к изданию; издание карт. 9.1.1. Редакционно-подготовительные работы. Включают проектирование карт, организационно-подготовительные работы, разработку редакционных документов. В процессе проектирования карт выполняется: 0 ... 21 22 23 24 25 26 27 ... 36 |












