Раздел: Документация
0 ... 19 20 21 22 23 24 25 ... 78 связи между данными. Более точно, рекурсии БПФ могут быть записаны как (с использованием вычислительной схемы "с замещением" [2]) x(m+1)(p) = х(т\р) + WNx<m\q), x<m+1\q) = xlm\p) - Kx(m\q), где p,q,r - параметры, изменяемые от стадии к стадии. Длина предполагаемой глобальной линии связи будет пропорциональна величине \р - q . На последней стадии достигается максимум длины, когда \р- q \ =N/2. (Например, для 1024-точечного БПФ эта максимальная величина равна 512.) Очевидно, алгоритм БПФ не может быть реализован в вычислителях со структурой локального типа, таких как систолические или волновые матрицы. Более интересным примером является проектирование БИХ-фильтров. В общем случае БИХ-фильтр характеризуется следующей передаточной функцией: n H(z) =-• i+ !>«*- i= 1 Трансверсальный фильтр есть просто частный случай БИХ-фильтра, когда знаменатель в Я(г) равен 1. Соответствующий рекурсивный алгоритм часто записывают в виде разностного уравнения yik) = V х(к - тЩт) + £ У(к ~~ т)а{т).(7Л) т-1т~ 1 Эта форма представления включает в себя глобальную индексацию и, таким образом, ведет к реализации алгоритма глобального типа в канонической форме [3, 4], показанной на рис. 7.2,а. Тем не менее эта схема легко может быть преобразована в схему локального типа; следовательно, также может быть преобразован и алгоритм, представленный уравнением (7.1). Видоизмененная схема показана на рис. 7.2,6. Для проверки того, что схема на рис. 7.2,а определяется той же самой передаточной функцией, что и схема на рис. 1.2,6, просто проверим передаточные функции у IN) fzyfj(.N) (z) и jv (АО (z)/£/(A0 (г ) .Очевидно, они не изменяются при модификации. По индукции, для i -N-l, N- 2, . . . , 1 можно показать неизменность передаточных функций Г (О (л) /(О (г), ц/0°) (z)/l70) (2), что и завершает доказательство. Следует отметить, что при видоизмененной прямой форме всегда имеются устройства задержки между сумматорами и поэтому требуются только локальные связи. 7.3.2. Систолическая матрица для ЬИХ-фильтрапии Покажем, что видоизмененная форма представления в действительности эквивалентна схеме систолической матрицы (рис. 7.3,с), за исключением масштаба времени. Так как задержка в половину единицы времени (г"1/2) не является общепринятой, дальнейшим шагом (рис. 7.3,е) является Изменение масштаба времени введением » • • Xj «2Tg xf *£q 4* 1 V> н-0 a) ... х3хгх, xe* -+>jHZD 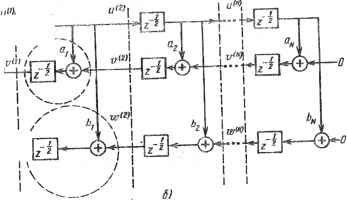 <?УоУг№з""*-"ft Рис. 7.2. Прямая форма проектирования БИХ-фильтра, требующая глобальных связей (о), и видоизмененная прямая <Ьорма с локальными связями (б) переменной z по формуле z~42=z*~1. При этом элемент задержки г", умножитель и сумматор в каждой секции, ограниченной штриховыми линиями на рис. 1.2,6, образуют ПЭ "скалярного произведения" [5] (рис. 7.3,б). Полная схема систолической матрицы, реализующей БИХ-фильтр, показана на рис. 7.3,е. Заметим, что из-за изменения масштаба времени входные данные {хЛ должны чередоваться с "пустыми" тактами (см. рис. 7.3,в), а скорость обработки становится равной 0,5 Т~1, Имея теперь локализованную матрицу, можно, в свою очередь, вывести локальную версию алгоритма (7.1). Обозначая верхним индексом временную переменную, а нижним индексом - пространственную, соответствующие движения данных в указанной систолической структуре можно представить следующими рекуррентными выражениями локального типа [при а (0) -Ь (0) -0] : п „Лч i - к /..1 .1. vk (7.2 а) (7.2 6) (7.2в) и+1 я справедливыми для всех и, кроме и =0, когда AT*+1 = (7.2 г) 137 а) 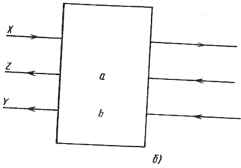 X хМ=х* Г z"*=z*+ax*
-о О в) Рис. 7.3. Изменение единицы времени z42=?~i , ч систолический матричный процессор для BHX-bTpaVeT"0"11460""3 № " Начальные условия имеют вид z°=o, г°=о. Граничными являются условия ZN+1 =0- ул<+1 =0-Входная последовательность записывается как Х2*-1=х(к),(7.3 а) выходная последовательность yf=y(k).(7.3 6) Интересно, что корректность систолической матрицы может быть легко установлена путем выполнения z-преобразования выражений (7.2) и (7.3) и некоторых тривиальных алгебраических преобразований. Заметим, что скорость обработки указанного систолического процессора равна 0,5т""1 (т.е. результат на выходе появляется только в один из каждых двух временных тактов). Эта скорость меньше той, которая получается при прямой форме реали-138 зации (1,0 У"1), поскольку только на передачу данных (А-»А ) требуется затратить один полный такт времени - столько же, сколько на операции умножения и сложения, что является ненужным расточительством. Имеется два способа решения этой проблемы. Первый состоит в использовании многоскоростной систолической матрицы, а второй - в использовании волновой матрицы, основанной на асинхронном, управляемом данными вычислении. 7.3.3.Многоскоростная систолическая матрица Многоскоростная систолическая матрица представляет собой обобщенную систолическую матрицу, в которой различные потоки данных могут передаваться через матрицу с различной скоростью, что позволяет выполнять различные основные операции за различное время. Если в примере с БИХ-фильтром принять Д за единицу времени при передаче данных, а Т - при умножении-сложении, то при z -преобразовании появятся две различные переменные Zj"1 и zj1, соответствующие задержкам Д и Т в схеме, приведенной на рис. 7.2,в, z~1/2 в прямых цепях (для X) заменится на z\~x, в цепях обратной связи (для Y и Z) - на zj1. Такое изменение приводит к многоскоростной систолической матрице, показанной на рис. 7.3,а, б. В этой схеме данные X движутся ритмично со скоростью 1/Д, а данные Y и Z - со скоростью 1 /7". Поскольку передаточной функцией процессорной матрицы будет ll(z " ), где z" =z1*1 +z J1, то входные {а0, Х\, х2 , •} и выходные {У о, У и У г ,} последовательности движутся со скоростью 1/(7"+Д). В соответствии с теорией реализации многоскоростных систем [18] одной и той же передаточной функции H(z" ) соответствует множество структур многоскоростных матриц. Это обстоятельство стоит подчеркнуть в связи с тем, что одни структуры могут быть в цифровом исполнении лучше других [18]. Многоскоростная систолическая матрица на самом деле представляет собой не что иное, как синхронизированную версию волновой матрицы (см. подразд. 7.3.4). Такая матрица может применяться при совмещенной порязрядной и пословной систолической или волновой обработке. Хорошим примером этого служит (синхронная) волновая матрица, реализующая алгоритм CORDIC для QR-разложения [12], где в квадратной процессорной матрице вертикальным волновым фронтом распространяются слова (многоразрядные), в то время как по горизонтали распространяются отдельные разряды. (В этом случае распространяемые по горизонтали разряды управляют углами поворота в алгоритме CORDIC [19].) 7.3.4.Волновая матрица БИХ-фильтра Когда проблема синхронизации систем становится критической, можно прибегнуть к волновому подходу, используя асинхронные, управляемые данными вычисления. Наша цель состоит теперь в замене вычислений в систолической матрице с глобальной синхронизацией на асинхронную, управляемую данными модель, показанную на рис. 7.4. Операция, соответствующая каждой вершине на рис. 7.4, выполняется тоща, и только тогда, когда готовы требуемые операнды. Так как обработка асинхронна, ссылка 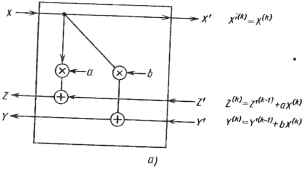 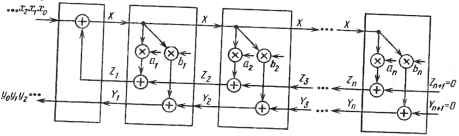 6) l27ZZ:VT ~Управляемая данными на время становится излишней. Непосредственным преимуществом этой модели является то, что передача данных (Х-*Х) занимает время, незначительное по сравнению с временем, необходимым для арифметической обработки. Точнее, достигаемая пропускная способноть при волновой обработке приблизительно равна 1,0Г"1 (т.е. в два раза выше, чем в чисто систолической матрице, предоставленной на рис. 7.3). Теперь мы имеем другой способ представления рекурсии. Для этого верхний индекс А (в круглых скобках) будем интерпретировать как номер волнового фронта (или номер рекурсии), так как индекс времени больше не нужен. Новое представление (7.1), имеет вид (в предположении, что в(0) =/; (0) =0) у<*> = *<*>ад + Y»+1»f(7.4а) Z№> = Ха(п) + Zif+V,(7.4 б) Х(к) = Х(к) + Zf.(7.4 в) Согласно (7.4в)инициируется в ведущем ПЭ (н = 0) и распрост- раняется вправо по процессорной матрице, активизируя операции (7.4 а) 140 (7.4 6) во всех управляемых данными ПЭ. Как показано на рис. 7.4, обновленные данные {Y{k)+l, Zjf] ,} подаются в обратном направлении для следующей рекурсии (или для следующего волнового фронта). Другой важной особенностью является то, что модели с управлением данными допускают использование простого потокового языка. На языке MDFL описание (для неограниченного поля ПЭ) имеет вид BEGIN
END Заметим, что приведенная программа записана на локальном уровне, т. е. в расчете на один процессорный элемент. После формального введения понятия волнового фронта можно использовать глобальный уровень языка MDFL, полагая, что «дин волновой фронт обрабатывается всеми процессорами. Представление алгоритма в виде последовательности волновых фронтов упрощает его понимание, и поэтому глобальный язык MDFL уменьшает трудности программирования. 7.4. ВОЛНОВАЯ МАТРИЧНАЯ ОБРАБОТКА С точки зрения нисходящего проектирования следует учитывать тот факт, что громадное большинство алгоритмов обработки сигналов обладает упомянутыми свойствами рекурсивности и локальности. В самом деле, большая часть вычислительных потребностей для обработки сигналов и прикладных математических проблем может быть сведена к основным матричным операциям и другим родственным алгоритмам [10, 11]. Свойственный этим алгоритмам параллелизм требует намного большей производительности параллельных вычислений, чем та, которую способна обеспечить одномерная матрица. Первым важным архитектурным достижением в этой области являются двумерные систолические структуры для матричного умножения, обращения матриц и т.п. (полный обзор читатель найдет в [6]). В этом разделе сосредоточим внимание на алгоритмическом анализе, который приведет к согласованному языковому и архитектурному проектированию, необходимому для двумерного матричного процессора. На самом деле именно алгоритмический анализ матричных операций впервые приведет нас к понятию двумерного волнового вычислительного фронта. Все рассмотренные ранее алгоритмы разлагаются на последовательные рекурсии 0 ... 19 20 21 22 23 24 25 ... 78 |
||||||||||||||||||||||||||||||||||||||||||||||||||||












