Раздел: Документация
0 ... 20 21 22 23 24 25 26 ... 78 и могут быть отображены в соответствующие волновые фронты в однородной вычислительной сети. (Волновой фронт соответствует одной стадии рекурсии) . Конвейеризация последовательности вычислительных волновых фронтов приводит к непрерывному продвижению волны данных и волны вычислительного процесса. 7.4.1. Последовательные математические рекурсии Проиллюстрируем последовательность математических рекурсий на примере матричных операций. Пусть Х = ац,Ь = Ъц,С = АХ В - матрицы размера NXN. Матрица А может быть разложена на столбцы Af, а матрица В - на строки В;-, и, следовательно, C=AlBl +А2В2 + ... + ANBN. Матричное умножение может быть осуществлено за А рекурсий: С?} = +(7.5а) а?1 = а* ,(7.5 б) ЬУ = Ь«,(7.5 в) где к=\, 2,..., А/, и это приводит к множеству из Л/ волновых фронтов. Конвейеризация вычислительных волновых фронтов [7]. Рассмотрим вычислительный волновой фронт для первой рекурсии в матричной операции умножения. Предположим, что регистры всех ПЭ в начальный момент установлены в нуль: С?> = 0 для всех (i, /). Исходные значения матрицы А хранятся в модулях памяти слева (в столбцах) , а матрицы В - в модулях памяти сверху (в строках). Процесс начинается с ПЭ, обозначаемого символом (1,1): сст;+ п11*ь11. Вычислительный фронт распространяется к ближайшим соседним ПЭ (1, 2) и (2, 1), которые будут выполнять параллельно операции С\Ч = С<°2» + а„ *Ь12, <%! = С<2°> + а21*Ьи . Следующий фронт активности будет у процессорных элементов (3, 1), (2, 2) и (1, 3). Так создается движущийся вниз по процессорной матрице вычислительный волновой фронт. Этот вычислительный волновой фронт подобен электромагнитному волновому фронту (оба они подчиняются принципу Гюйгенса), так как каждый процессор действует как источник вторичного излучения, создающий движущийся волновой фронт. Заметим, что при распространении волны предполагается локализованный поток данных. После того как волновой фронт проходит через все ячейки ПЭ, первая рекурсия считается выполненной (рис. 7.5). По мере распространения первой волны можно выполнить вторую ре- рис. 7.5. Двумерная волновая структура: д единица времени переда*™ данных; Т единица времени выполнения операции Модули памяти Код программы] Память Кгр Г/ я» / Г У/ . V V .Кл- Л/ -4/ /у. LZ- J. id Ль Первая волна---- Вторая волна---- курсию параллельно поточной организацией второго волнового фронта немедленно после первого. Например, процессор (/, /) будет выполнять операцию С<2) =C(i) + а *Ь Ч/1/ ы1г uzj и т.д. Конвейеризация возможна потому, что волновые фронты двух последовательных рекурсий никогда не пересекаются, так как в каждый момент времени выполняющие рекурсию процессоры будут различны и тем самым устраняются любые проблемы гонок. Напомним, что волновые фронты могут распространяться различными способами. Важно только, чтобы точно соблюдался порядок последовательных действий. Это правило обеспечивается природой потоковой волновой обработки. Поэтому реальный способ распространения практически не имеет значения. В действительности при использовании локальной синхронизации волновой фронт может быть криволинейным и тем не менее будет обеспечена правильная последовательность вычислений. 7.4.2. LU-разложение При Ш-разложении данная матрица С должна быть представлена в виде С = АХВ,(7.6) 143 где А - нижняя, а В - верхняя треугольные матрицы. Рекуррентные выражения имеют вид С}5> = С1Г1)-а%Г,(7.7а) "P-icf.",(7.76) скк *f-=Cfcj.(7-7 в) где Л = 1,2,... ,А; к <i <N; k<j <N. Проверяя процедуру посредством вычислений по формуле (7.7а) в обратном порядке, убеждаемся в том, что С = с}?>=- АВ, *-=i где А= = {я}, В = {b} = {fcs} - матрицы на выходе системы обработки (сравните с (7.6)). Сравнение (7.5) и (7.7) указывает на сходство этих процедур. В действительности, волновой фронт для LU-разложения (7.7) будет аналогичен волновому фронту на рис. 7.6, за исключением следующего: 1.Так же, как и при матричном умножении, данные а© и распространяются вправо и вниз соответственно. Однако в© получается в результате вычислений, что вызывает дополнительную задержку; см. (7.76) [в то время как прямо получается из предыдущей рекурсии; см. (7.7в)]. 2.В самой простой схеме вторая рекурсия может начинаться в ПЭ (2, 2) [третья в ПЭ (3, 3) и т.д.]. Тем не менее для удобства аппаратной реализации все рекурсии лучше начинать в ПЭ (1, 1). В любом случае активное пространство обрабатывающей структуры сжимается (сокращается) от одной рекурсии к другой. (Это неизбежно приводит к некоторым потерям в эффективности использования процессора [7].) 7.4.3. Нахождение собственных значений с помощь» волновой обработки Во многих случаях применения обработки сигналов, таких как спектральное оценивание при формировании луча с высоким разрешением, сжатие данных об изображении и т.д. [20, 21], алгоритмы определения собственных значений сингулярных чисел матриц выступают как чрезвычайно мощный эффективный инструмент. Согласно [22] "QL и QR-алгоритмы... являются наиболее эффективным способом получения всех собственных значений небольших симметрических матриц". Может ли QR-алгоритм сохранять зту эффективность при отображении его в виде некоторого параллельного алгоритма на квадратную или линейную многопроцессорную структуру? Ответ на .?тот вопрос будет дан в следующем разделе с помощью понятая вычислительного волнового фронта. 7.4.4. Линейная ьпюгочроцессоркая структура для приведения симметрической матрицы к трехдиагошл&ному виду Вначале согласно QR-алгоритму матрица путем последовательных преобразований приводится к трехдиагональному виду, а затем согласно QL [QR]-144 алгоритму быстро уменьшается значение внедиагональных элементов до тех пор, пока они не станут пренебрежимо малыми. На каждом шаге алгоритма к предыдущему результату применяется довольно сложное преобразование подобия, что дает последовательность матриц, сходящуюся к диагональной матрице [22]. Приведение к трехдиагональному виду симметрической матрицы А= {а{г, /)} выполняется с помощью преобразования подобия: W=Q*A*Qr, где W - трехдиагональная, Q - ортогональная матрица. Как правило, Q является произведением А--2 ортогональных матриц: q = q(A-2)#q(/V- 0. ... »Q(2>. Q(i), таких, что Q<P) обращает N-p-l нижних элементов в р-м столбце матрицы А в нуль. Аналогично [Q(P) ]т обращает в нуль А-р- 1 верхних правых элементов в р-й строке матрицы А. Требование локальности, которое обсуждалось ранее, обусловливает применение вращений Гивенса для приведения матриц к трехдиагональному виду. Упомянутый оператор Q(P), по существу, вновь разбивается на последовательность операторов Q(* Р), каждый из которых обращает в нуль элемент а (а, р) Итак, Q>> =Q(P+2-P) *Q(P+3,P) * .. ..QW р) . Каждый оператор Q(<7-P) представляется в форме столбцы: q - 1 qстроки: Я - 1 )(«, р) C(q, р) %, р) -S(q,p) C(q, р) 1 1 Важно учитывать следующее: 1. Умножение слева матрицы А на Q<*- Р> изменяет только ц - 1-ю и q-ю строки матрицы А. После операции вращения элементы этих двух строк принимают следующие значения:
C(q, р) S(q, р) L -S(q, p) C(q, p) ar(q - И ar(q) где a1 - вектор-строка произведения Q <e> P> А. Заметим, что a (a, p) = 0. 2. Умножение справа A2 = (QXA) на Qr изменяет столбцы матрицы A2 с номерами q -1 и q, которые принимают значения C(q, р) S(q, Р) -S(q,p) C{q, Р) 12 13 ID 16 rn i£j ш и r*i [Те 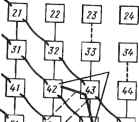 25 26 35 36 65 66 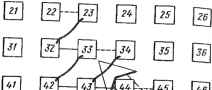 ш} 62 el] %] ТяГ 56 51 66 61 £]-£jj-£4-± 55 \ 551-5/5 I-A I-1 £5 -66 Рис. 7.6. Распространение строчного волнового фронта Рис. 7.7. Распространение столбцового волнового фронта где а"с(к) с v.vj - вектор-столбец матрицы А20. Так как А - симметрическая матрица, эта операция является в основном повторением многих операций со строками в процессе умножения QXA. Исключениями являются четыре элемента, расположенные на пересечении строк и столбцов q и q - 1. 3. Последовательность операций не является жесткой, и поэтому допустима конвейеризация волнового фронта. Характеризуя волновые свойства этого процесса, можно различить волны двух типов. К первому типу относятся волны, связанные с операциями над строками, так называемые строчные волны, а ко второму тану - волны, связанные с вычислениями на границах и операциями над столбцами. Последние могут рассматриваться как отраженные волны, движущиеся вдоль диагонали, и в дальнейшем будут называться столбцовыми. (Учитывая симметрию задачи, можно удалить ПЭ выше главной диагонали., сохранив треугольную структуру без потерь какой-либо информации.) {.Распространение строчного волнового фронта. Природу волнового фронта можно понять из рис. 7.6, на котором изображены фронты активности, связанные со строчными операциями, приводящими к обнулению элементов первого столбца. 2. Распространение столбцового волнового фронта. На рис. 7.7 показана последовательность столбцовых волн. Первый столбцовый волновой фронт может быть инициирован тогда, и только тогда, когда первая строчная волна достигает конца (т.е. последних двух элементов в последних двух строках) . Первая задача этого фронта состоит в изменении содержимого столбцов с номерами А и А- ] с помощью оператора [QO Jт. Столбцовая волна может продвигаться на один шаг после того, как строчная волна закончила операции с последними элементами строк А- 1 иЛ-2. В процессе вычислений операции над строками с номерами q и q - 1 должны заканчиваться 146 доначала соответствующих операций над столбцами. Это следует из того, что операции над столбцами требуют данных, которые являются выходными в операциях над строками. Аналогично операции над столбцами, соответствующие обращению в нуль (N-p - 1) элементов строки (строчная волна), должны заканчиваться до начала операций над строками, относящихся к обращению в нуль столбца р +1 (столбцовая волна р + 1). Из рис. 7.6 и 7.7 можно, таким образом, увидеть, что по сути дела в любой момент времени самое большее два ПЭ в каждом столбце активно выполняют операции вращения. Поэтому предлагаем применять описанную процедуру, используя структуру процессорных элементов линейного или билинейного вида. Вычислительные задачи назначаются ПЭ так, что первая строка ПЭ формирует параметры и выполняет операции над строками, в то время как вторая строка ПЭ выполняет операции над столбцами. Хотя физическая конфигурация процессорной матрицы изменилась от квадратной к линейной, природа вычислительного волнового фронта осталась неизменной и теоретическое направление распространения вычислительной активности сохранилось. Таким образом получено отображение виртуальной квадратной конфигурации в билинейную структуру реальной машины. Отметим, что билинейная структура будет обеспечивать время выполнения О (А2), как и квадратная (или треугольная), что доказывает ненужность последней. Одним из самых популярных методов определения собственных значений симметрической трехдиагональной матрицы является итерационный метод диагонализации. Он состоит в серии простых преобразований подобия, в результате которых сохраняются симметричность и ленточность матрицы и в то же время уменьшаются значения внедиагональных элементов, что приводит матрицу к диагональному виду с элементами, которые и являются искомыми собственными значениями. Этот алгоритм может быть легко отображен на линейную процессорную матрицу с волновой обработкой [12, 13]. В связи с нехваткой места для детального обсуждения волновой обработки при вычислении собственных значений и сингулярных чисел и решении теплицевых систем рекомендуем читателю для ознакомления с этими вопросами обратиться к работам [13 - 15]. Эти методы представляют также интерес применительно к решению проблемы формирования луча с высоким разрешением [20]. 7.4.5. Применение волновой обработки Понятие волновой обработки применимо ко всем алгоритмам, которые обладают рекурсивностью и локальностью. Такие алгоритмы могут быть разбиты на три группы. 1. Алгоритмы основных матричных операций [7, 13]: матричное умножение; LU-разложение; вращение Гивенса; обратная подстановка; обращение матриц; определение собственных значений; определение сингулярных чисел. 0 ... 20 21 22 23 24 25 26 ... 78
|
