Раздел: Документация
0 ... 65 66 67 68 69 70 71 ... 78 же время они поэтапно преобразуются в большие по размерам и более глобальные подобъекты). Таким образом, древовидная структура из большого числа простых и локальных детекторов элементов изображения может служить для распознавания больших и сложных объектов. По объему сообщений размер пирамиды О (log N) является существенным улучшением в сравнении с размером матрицы О(N). Действительно, на практике при обработке изображений размером от 256X256 до 1024X1024 элементов это является существенным различием. Матричные, конвейерные и в особенности пирамидальные структуры обеспечивают увеличение производительности и вычислительной мощности на несколько порядков по сравнению с традиционными ЭВМ с одним централ ь-ным процессором. Представляется, что они особенно пригодны для обработ-ки изображений, распознавания образов и в системах технического зрения. Они также хорошо соответствуют требованиям технологии СБИС благодаря своей регулярной микромодульной структуре. СПИСОК ЛИТЕРАТУРЫ [1] К. Е. Batcher, " Design of a Massively Parallel Processor," IEEE Trans. Comput., 29:836-840(1980). [2] A. M. Despain and D A. Patterson, "X-Tree: a Tree Structured Multi-processor Computer Architecture," Proc. 5th Annu. Symp. Comput. Arch., Apr. 1978, pp. 144-151. [3] M. J. B. Duff, CLIP4: "A Large Scale Integrated Circuit Array Parallel Processor," Proc. IJCPR-3, 4:728-733 (1976). [4] M. J. B. Duff, personal communication, 1982. [5] C. R. Dyer, "Pyramid algorithms and machines," in: K. Preston, Jr., and L. Uhr, eds., Multicomputers and Image Processing, Academic Press, New York, 1982, pp. 409-420. [6] D. J. Farber and К. C. Larson, "The System Architecture of the Distributed Computer System-The Communications System," Symp. Comput. Networks, Polytechnic Institute of Brooklyn, Apr. 1972. [7] R. A. Finkel and M. H. Solomon, "Processor Interconnection Strategies," Comput. Sci. Dept. Tech. Rep. 301, University of Wisconsin, 1977. [8] R. A. Finkel and M. H. Solomon, "The Lens Interconnection Strategy," Comput. Sci. Dept. Tech. Rep. 387, University of Wisconsin, 1980. [9] J. R. Goodman and A. M. Despain, "A Study of the Interconnection of Multiple Processors in a Data Base Environment," Proc. 1980 Int. Conf. Parallel Process., 1980 pp. 269-278. [10] A. R. Hanson and E. M. Riseman, "A Progress Report on VISIONS," COINS Tech. Rep. 76-9, University of Massachusetts, 1976. [11] E. W. Kozdrowicki and D. J. Thies, "Second Generation of Vector Supercomputers " Computers, /5:71-83 (Nov. 1980). [12] B. Kruse, "The PICAP Picture Processing Laboratory," Proc. IJCPR-3 4 875-881 (1976). [13] M. D. Levine, "A Knowledge-Based Computer Vision System," in A. Hanson and E. Riseman, eds., Computer Vision Systems, Academic Press, New York, 1978, pp. 335-352. [14] G. A. Mago, "A Cellular Computer Architecture for Functional Programming," Proc COMPCON Spring 1980, 1980, pp. 179-187.fx 412\X [15] R. Manara and L. Striftga, "The EMMA System: An Industrial Experience on a Multiprocessor," in M. J. B. Duff and S. Lerialdi, eds., Languages and Architectures for Image Processing, Academic Press, London, 1981. [16] S. F. Reddaway, "DAP-A Flexible Number Cruncher," Proc. 1978 LASL Workshop Vector Parallel Process., Los Alamos, 1978, pp. 233-234. [17] s. F. Reddaway, personal communication, 1982. [18] A. Rosenfeld, ed., Multi-resolution Systems for Image Processing, North-Holland, Amsterdam, 1983, in press. [19] H. J. Siegel, "A Model of SIMD Machines and a Comparison of Various Interconnection Networks," IEEE Trans. Comput., 28:901 917(1979). [20] H. J. Siegel, "PASM: A Reconfigurable Multimicrocomputer System for Image Processing," in M. J. B. Duff and S. Levialdi, eds., Languages and Architectures for Image Processing, Academic Press, London, 1981. [21] W. Snapp, personal communication, 1982. [22] S. R. Sternberg, "Cytocomputer Real-Time Pattern Recognition," 8th Pattern Recognition Symp., National Bureau of Standards, 1978. [23] S. R. Sternberg personal communication, 1982. [24] H. S. Stone, " Parallel Processing with the Perfect Shuffle," IEEE Trans. Comput., 20:153 161 (1971). [25] H. Sullivan, T. Bashkov, and D. Klappholz, "A Large Scale, Homogeneous, Fully Distributed Parallel Machine," in Proc. 4th Annu. Symp. Comput. Arch., 1977, pp. 105-124. [26] R. J. Swan, S. H Fuller, and D. P. Siewiorek, "Cm*-A Modular, Multi-microprocessor," Proc. AFIPS NCC, 1977, pp. 637-663. [27] S. L. Tanimoto, "Towards Hierarchical Cellular Logic: Design Considerations for Pyramid Machines," Computer Science Dept. Tech. Rep. 81-02-01, University of Washington, 1981. [28] S. L. Tanimoto, " Programming Techniques for Hierarchical Parallel Image Processors," in K. Preston, Jr., and L. Uhr, eds., Multi-computers and Image Processing, Academic Press, New York, 1982, pp. 421 429. [29] S. L. Tanimoto and A. Klinger, eds., Structured Computer Vision, Academic Press, New York, 1980. [30] S. L. Tanimoto and J. J. Pfeiffer, Jr., "An Image Processor Based on an Array of Pipelines," Proc. Workshop on Computer Architecture for Pattern Analysis and Image Data Base Management, IEEE Computer Society Press, 1981, pp. 201-208. [31] K. J. Thurber, Large Scale Computer Architecture, Hayden, Rochelle Park, N.J., 1976. [32] L. Uhr, " Layered 4 Recognition Cone Networks That Preprocess, Classify and Describe," IEEE Trans. Comput., 27:758 768 (1972). [33] L. Uhr, "1Recognition Cones and Some Test Results," in A. Hanson and E. Riseman, eds.. Computer Vision Systems, Academic Press, New York, 1978, pp. 363-372. [34] L. Uhr, "Converging Pyramids of Arrays," Proc. Workshop on Computer Architecture for Pattern Analysis and Image Data Base Management, IEEE Computer Society Press, 1981, pp. 31 34. [35] L. Uhr, Algorithm-Structured Computer Arrays and Networks: Parallel Architectures for Perception and Modelling, Academic Press, New York, 1984. 413 [36] L. Uhr, "Pyramid Multi-computer Structures, and Augmented Pyramids," in M. Duff, ed., Computing Structures for Image Processing, Academic Press, London, 1983, in press. [37] L. Uhr, "Pyramid Multi-computers, and Extensions and Augmentations," in D. Gannon, H. J. Siegel, L. Siegel, and L. Snyder, eds., Algorithmically Specialized Computer Organizations, Academic Press, New York, 1984, in press. [38] L. D. Wittie, "MICRONET: A Reconfigurable Microcomputer Network for Distributed Systems Research," Simulation, 57:145-153 (1978). ПАРАЛЛЕЛЬНЫЕ АЛГОРИТМЫ ДЛЯ АНАЛИЗА ИЗОБРАЖЕНИЙ А. Розенфелд1 24.1. ВВЕДЕНИЕ В системах обработки и анализа изображений (ОАИ) используется широкий круг методов кодирования, преобразования, сегментации и измерения характеристик изображения. Многие из этих методов пригодны для эффективной параллельной обработки. В данной главе рассматриваются некоторые основные классы алгоритмов ОАИ и демонстрируется, как такие алгоритмы могут быть распараллелены и реализованы на различных видах ячеечных многопроцессорных систем. По тематике ОАИ выпускается много литературы. Имеется как минимум дюжина учебников [1 - 12], охватывающих основную часть предмета, не считая книг по конкретным проблемам и подборок статей. Последний библиографический ежегодник приведен в статье [13]; он охватывает в основном не ориентированную на приложения американскую литературу и включает до 1000 наименований в год. Ссылки на конкретные алгоритмы (классы алгоритмов) в данной главе не приводятся. Около 25 лет назад было впервые высказано предположение [14] о возможности параллельной реализации алгоритмов ОАИ в машинах с ячеечной матричной структурой (рис. 24.1) - двумерной матрицей процессоров (ячеек) , работающих синхронно и связанных каждый со своими соседями в матрице. Было построено несколько машин такого типа с размером матриц до 128X128. Было разработано множество алгоритмов ОАИ, подходящих для реализации на ячеечных матрицах (общие сведения можно найти в работах [15, 16]). В последнее время наметился интерес к использованию пирамид ячеечных матриц размером 2пХ2п, 2п~1Х2п~19 . . . , 2X2, 1X1, где каждая ячейка связана не только со своими соседями-братьями на собственном уровне, но также и с четырьмя своими "детьми" на уровне, расположенном ниже, и "родителем" на верхнем [15,17] (рис. 24.2). 1 Мэрилендский университет, Колледж-Парк, Мэриленд. 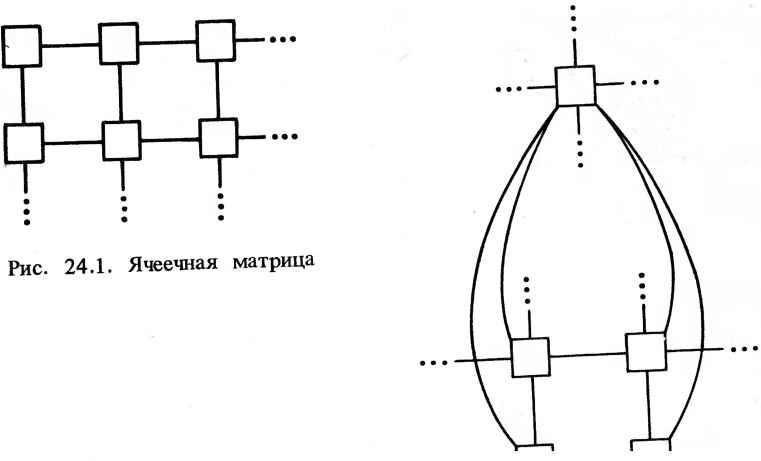 Уровень I + 1 ... Уровень I Рис. 24.2. Ячеечная пирамида•" Ячеечные матрицы или пирамиды пригодны для выполнения многих типов операций ОАИ на уровне элементов растра. С другой стороны, в некоторых операциях анализа изображений, выполняемых над участками изображения, используются не матрицы элементов растра, а некоторые другие структуры данных для представления участков и их связей. Для таких операций больше подошел бы более общий класс матричных машин графояче-ечной структуры, в котором ячейки, соответствующие узлам графа, связаны со своими соседями в соответствии с дугами графа. О таких графояче-ечных машинах можно прочесть в [18, 19]; об архитектуре систем, соответствующих более частным типам структур данных, см. [20 - 22]. 24.2. ОБРАБОТКА НА УРОВНЕ ЭЛЕМЕНТОВ РАСТРА Любой цифровой образ есть прямоугольная матрица элементов растра. Элемент является, как правило, целочисленным (наиболее часто используется 8-разрядное целочисленное представление), но может быть представлен также в вещественной, комплексной и векторной форме (в случае цветного изображения). В данном разделе описываются алгоритмы обработки матриц элементов растра. 24.2.1. Точечная и локальная обработка Большинство операций, обычно выполняемых при ОАИ, преобразуют изображение в изображение, при этом значение элемента в выходном образе зависит только от значения соответствующего элемента и, возможно, некоторых близлежащих элементов во входном образе или образах. Примером таких операций являются: 415 1)увеличение контрастности с помощью тонового преобразования; при этом новое значение элемента зависит только от его прежнего значения, определенного исходным заданием; 2)увеличение резкости, например, с помощью лапласовской фильтрации, основанной на различии между значением элемента и средним уровнем значений соседних с ним элементов; 3)сглаживание локальным усреднением (нахождение усредненного, возможно, взвешенного значения элемента и некоторых соседних с ним элементов), с помощью медианной фильтрации или усреднением множества изображений и т.д.; 4)сегментация путем сравнения с порогом (элемент принимает новое значение 1 или 0 в зависимости от того, превышает ли прежнее значение установленный порог) или, в более общем виде, в соответствии с классификацией элементов по набору характеристических величин (по компонентам цветности, локальным характеристикам и т.д.); 5)выделение контура (или другой локальной характеристики), основанное на вычислении разности значений соседних элементов; 6)расширение или сжатие; новое значение элемента является максимальным или минимальным в группе значений окружающих его элементов (в некоторых случаях, например при изменении ширины, перед изменением элемента должны быть соблюдены дополнительные условия). Отметим, что некоторые из этих операций линейны и поэтому являются свертками, но большинство - нет. Операции этих типов могут очень эффективно выполняться на ячеечных матричных машинах, содержащих в идеале по процессору на каждый элемент. Каждый из процессоров собирает данные от своих соседей, а затем вычисляет требуемую функцию от этих величин. Необходимое для этого время зависит от размеров окружающих элементов и сложности операции, но не от размеров изображения. Если не имеется достаточного числа процессоров, то изображение можно обрабатывать поблочно, используя необходимое перекрытие между блоками для устранения граничных эффектов. 24.2.2. Преобразования т Над изображениями часто выполняются различные виды интегральных преобразований (или их дискретных вариантов) ; наиболее общим их примером является преобразование Фурье. В .случае преобразований выходным изображением также является матрица того Же размера, что и входная, но соответствия между их элементами уже нет. Преобразования обычно разделимы так, что они могут производиться сначала по строкам, а затем по столбцам; тогда значение нового элемента является линейной комбинацией значений элементов строки (или столбца) изображения. При выполнении преобразований на обычной ЭВМ можно использовать эффективные алгоритмы, например быстрое преобразование Фурье, для которого требуется 0(п log п) операций вместо 0(п2) по каждой строке или столбцу; общий объем вычислений для изображения размером пХп при 416С\ этом составляет 0(п2 log п). Здесь игнорируются проблемы доступа к изображению, располагаемому во внешней памяти, а также возможной необходимости в транспонировании изображения для обеспечения эффективного достутта к нему как по строкам, так и по столбцам. В ячеечной матричной машине строки или столбцы могут преобразовываться параллельно, а время, необходимое для преобразования каждой строки, равно 0(п) (каждый элемент должен быть перемножен на п коэффициентов, а результаты умножения сгруппированы и просуммированы); таким образом, общее время преобразования также равно О (п). Над изображением можно выполнить много полезных типов операций, например свертку, выполняя прямое преобразование Фурье, перемножая поточечно его результаты на соответствующие весовые функции (или поточечно перемножая преобразования двух изображений), а затем выполняя обратное преобразование Фурье над результатами для получения обработанного изображения. При этом общее время преобразования матричной машины также составит всего 0(п). Для сверток с большим числом весов это может оказаться более эффективным, чем непосредственное выполнение свертки при параллельном сборе информации о близлежащих элементах. 24.2.3. Геометрическая обработка Следующий класс операций типа "изображение-изображение" использует геометрические преобразования изображений (например, масштабирование, вращение или произвольную "деформацию" для корректирования геометрических искажений или сличения с другим изображением). В данном случае выходные элементы растра соответствуют входным, но не один к одному (даже такое преобразование, как вращение, будучи выполнено в цифровой форме, не дает однозначного соответствия). Для выполнения таких преобразований над некоторым изображением следует вычислить для каждого элемента выходного растра соответствующую позицию во входном (которая в общем случае не совпадает с позицией входного элемента). Затем следует присвоить значение этой выходной позиции, интерполировав значения близлежащих входных элементов. Основой метода выполнения геометрических преобразований в ячеечной матричной машине является закрепление за каждым процессором выходного элемента и сканирование входного изображения таким образом, чтобы каждый процессор мог получить входные величины, необходимые ему для вычисления выходных. Для иллюстрации того, как это может быть сделано за 0(п) шагов, обозначим через множество входных элементов, необходимых для вычисления выходного элемента (/,/); пусть Rj обозначает г-ю строку, a Cj - /-й столбец. Будем считать, что для всех i и/ множество I(Ц-ЗПТ! ограничено, т.е., другими словами, число входных элементов в данной строке Ri9 значение которого требуется знать для выходных элементов в данном столбце Су, ограничено. (Это утверждение не является справедливым для всех возможных преобразований; например, оно ложно для операции транспонирования. Тем не менее для любого общепринятого гео- 0 ... 65 66 67 68 69 70 71 ... 78 |












