Раздел: Документация
0 ... 66 67 68 69 70 71 72 ... 78 метрического преобразования существует такая пара направлений - не обязательно по строкам и столбцам, для которой аналогичное условие выполняется.) Затем циклически сдвинем входные данные по строкам, дав возможность каждой ячейке собрать все данные в множество In /1 по мере продвижения, а собранные данные циклически сдвинем по столбцам так, чтобы каждая ячейка (/,/) выбрала необходимые ей величины, т.е. величины из множества Sjj. 24.2.4. Измерение характеристик Теперь рассмотрим операции преобразования входного изображения не в выходное, а в набор значений характеристик изображения. Примерами таких операций являются: 1)определение наличия или отсутствия конкретного значения элемента растра или расчет статистических характеристик (минимального, максимального, медианного значений, диапазона, среднеквадратического отклонения и т. д.); 2)подсчет числа появлений конкретного значения, например: число единиц в двоичном изображении характеризует площадь единичных значений; число возможных значений определяет гистограмму тонового изображения; число пар элементов с данным относительным расположением, характеризуемых возможной парой значений, определяет "матрицу совместных реализаций" изображения, которая полезна при описании его текстуры. Отметим, что в двух последних случаях участвуют к или к2 характеристик, где к - число тонов; 3)подсчет числа связанных участков из элементов, имеющих определенное значение; это стандартный метод подсчета объектов в сегментированном изображении. В ячеечной матричной машине объем таких операций составляет 0(п), так как для подсчета значений элементов растра и статистических вычислений нужно сконцентрировать их в одном месте, а это требует для организации связи дополнительного числа шагов, пропорционального размеру матрицы. Подсчет связанных участков требует предварительных шагов вычислений, при выполнении которых число элементов каждого из участков сокращается до одного, но это также может быть выполнено за время О (п) при использовании специальных процессов сжатия. Статистические вычисления и подсчет в пирамидальной матричной машине (см. разд. 24.1) могут быть выполнены за время О (log п). Значение каждого элемента передается "родителю", который подсчитывает или объединяет значения, полученные от его "детей", и передает результаты своему "родителю"; таким образом, через log п шагов (число уровней) ячейка на вершине пирамиды получает окончательное требуемое значение. Отметим, что в этом процессе используются только вертикальные связи между уровнями пирамиды, но не используются собственные связи данного уровня; таким образом, для преобразования требуется только ячеечная древовидная машина, в которой элементы растра расположены как листья. Подсчет связанных участков требует горизонтальных связей \в основании иирами- ды для выполнения шагов сжатия, которые тоже выполняются за время О (п); следовательно, пирамида не обеспечивает больших преимуществ при подсчете числа участков, а также не дает большого выигрыша при выполнении операций типа "изображение-изображение". 24.3. ОБРАБОТКА НА УРОВНЕ РЕГИОНОВ 24.3.1. Представление регионов Участок изображения (регион), или фактически любой набор его точек, может быть представлен двоичным изображением-маской, в котором все точки, принадлежащие набору, имеют значение 1, а все другие - значение 0. Такое представление имеет то преимущество, что находится в определенном соответствии с исходным изображением, однако его недостатком является необходимость в памяти объемом п2 независимо от сложности данного региона. Регионы могут представляться и другими способами, при которых для представления простых регионов требуется меньший объем памяти. Более того, можно вычислять свойства регионов и получать новые регионы из данных, обрабатывая непосредственно представления. Выполнение таких операций также можно реализовать параллельно, но при этом архитектура процессорной матрицы уже не будет для этого подходить, так как представления теряют подобие с матрицами. В данном подразделе рассматриваются некоторые стандартные представления регионов и возможности их параллельной обработки при использовании соответствующих многопроцессорных систем. Регион может быть определен указанием его границ (он может иметь более одной границы при наличии дыр); для каждой из границ необходимо указать координаты начальной точки, а также последовательность кодов, определяющих перемещения от точки к точке по границе [3 бита на перемещение, поскольку последовательные элементы растра являются соседними и имеют всего по восемь непосредственных соседей (рис. 24.3,я, б)]. Естественная архитектура для параллельной обработки граничных кодов [20] состоит из процессоров, объединенных в кольцевые структуры, где каждое из колец представляет границу (по процессору на код). Время вычисления в последовательной машине характеристик регионов, представленных таким образом, составляет О (га) , где га - длина границы; однако некоторые задачи, время последовательного решения которых составляет О (га2), могут быть выполнены за время О (га) в системе кольцевой структуры (например, вычисление граничных кодов объединения или пересечения двух объектов, заданных граничными кодами). Другим способом представления региона является отображение каждой строки его изображения в виде ряда проходов последовательностей нулей, заменяемых на последовательности единиц. Каждая строка определяется указанием начального значения (1 или 0) и длин последовательностей (рис. 24.3,в). Характеристики региона и коды длин последовательностей производных регионов могут вычисляться непосредственно из кодов заданного региона. Простая схема для параллельной обработки проходов может сос- 0210303332322515 В) 0:8 0:8 0:2, 1.5 0:6,2 0:6, 2 0:6, 2 0:5,3 0:5, 3 б) 2 2 4 2 5 3 г) 2 О 1 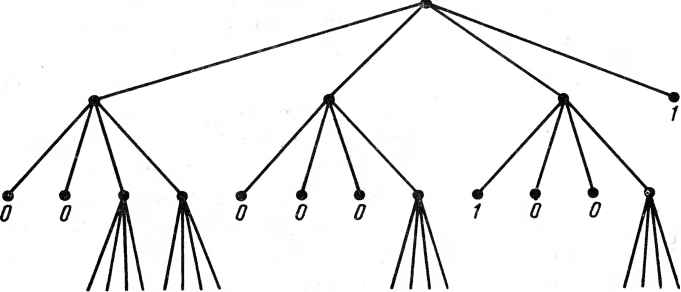 10 110 0 11 0 0 11 10 0 1 д) Рис. 24.3. Представления регионов: а - регион (единицы) ; б - коды границ (по часовой стрелке, начиная слева сверху); i = 90/, а i обозначает к повторений; в - коды длин последовательностей: для каждой строки за обозначением первого элемента растра следует список длин последовательностей; г - преобразование осей: центры (х, у) и радиусы (г) максимальных блоков; левый нижний угол изображения (0,0); д - квадродерево: порядок "сыновей" каждого узла, , , . Узлы-листья помечены их значением тоять из строк процессоров, каждая из которых содержит длины для соответствующей строки растра. Большую эффективность можно получить при установлении прямых связей между строками процессоров, представляющими соседние строки растра, где каждый из процессоров, представляющих заданную строку растра, непосредственно связан с процессорами, представляющими прилегающие строки. Такой подход к параллельной обработке регионов нельзя считать достаточно полно исследованным (см. [21]). Проходы - это горизонтальные "полоски" максимальной длины из элементов растра с постоянными значениями; более компактной формой представления региона является использование двумерных блоков элементов растра с постоянными значениями. Каждый из таких блоков определяется указанием его центра и радиуса, а регион является объединением блоков (рис. 24.3,г). Такое представление было предложено около 20 лет назад, однако оно не применялось сколько-нибудь широко, поскольку по нему трудно вычислить характеристики региона или поручить новые регионы непосредственно из-за перекрытия блоков и их несистематического распо-420 ложения. В некоторых случаях может оказаться возможным представление региона в виде "обобщенныхлент" где каждая лента есть объединение наибольших блоков, центры которых лежат на некоторой кривой. Такое представление гораздо более продуктивно, и обработка может вестись параллельно за счет размещения кода (т.е. последовательности перемещений и соответствующих радиусов) каждой кривой в строке процессоров; такая возможность еще не исследовалась. Другой тип представления региона максимал ьными блоками может быть основан на рекурсивном разбиении заданного двоичного образа на квадранты, подквадранты и т.д. до получения блоков постоянных размеров. Полученная структура блоков может быть представлена деревом 4-й степени (квадродеревом), в котором маршрут соответствует целому образу, а узлы-потомки - его квадрантам (рис. 24.3,д). Для изображения размером пХп, где п - степень числа 2, высота дерева не превышает log2 п, а каждый лист дерева представляет блок изображения, целиком состоящий из нулей или единиц. Характеристики региона и квадропредставления производных регионов могут вычисляться из квадропредставлений заданных регионов при последовательном обходе дерева. Для параллельного выполнения данных операций могут быть эффективно использованы квадро объединения процессоров [22]. Для представления многомерных изображений в виде объединений однородных блоков (например, блоков с постоянными значениями или блоков, в которых среднеквадратическое отклонение значений элементов растра невелико) можно использовать обобщенный вариант данного подхода, при котором блок делится на квадранты тогда и только тогда, когда он неоднороден. 24.3.2. Характеристики и отношения регионов Описанные представления регионов особенно полезны при работе с базами данных регионов (например, в цифровой картографии). При анализе изображений такие представления используются для измерения характеристик регионов и получения новых регионов из заданных. В этом разделе рассмотрим более абстрактный уровень обработки, при котором регионы не полностью определены, а представлены перечнями их характеристик. На этом уровне разбиение изображения может быть представлено в виде графа, узлы которого соответствуют регионам, отмеченным списком значений характеристик, а дуги - связанным парам регионов (например, прилегающих) отмеченных значениями отношений (например, длиной общей границы). Простой пример приведен на рис. 24.4. Разбиение может быть модифицировано слиянием пар регионов, основанным на информации, даваемой представлением в виде графа, без необходимости обращения к исходному изображению; граф нового разбиения может быть построен непо средств енно из заданного. Например, предположим, что граф содержит информацию о площади, периметре и среднем значении элементов растра каждого региона, а также длину общих границ каждой пары прилегающих регионов. Возможные критерии слияния пар прилегаю- 00000000 0 0 1 0 0 0 0 0 1 о о 1 о о 1 о о ООО ООО а)  ших регионов могут быть следующими: их средние значения весьма близки; их площади сильно различаются; длина общей границы составляет большую часть длины их периметров (или одного из них). Эти критерии могут быть проверены непосредственно по графу. Более того, если мы решили слить два региона, то можно построить новый граф непосредственно из старого замещением двух старых узлов одним, связанным со всеми соседями старого узла. Характеристики нового узла могут быть вычислены следующим образом: его площадь равна сумме площадей старых узлов; среднее значение его элементов является взвешенным средним старых значений пропорционально площадям; его периметр является суммой старых, из которой вычитается длина общей границы. Наконец, длина общей границы между новыми узлами и их соседями может быть вычислена непосредственно из длин границ старых узлов; они остаются прежними, за исключением случая, когда старые узлы имели общих соседей, и обе длины должны суммироваться. > Процесс слияния регионов, подобный описанному, может быть выполнен параллельно при использовании сети процессоров, в которой каждому региону приписан процессор, и процессоры, соответствующие прилегающим узлам, могут связываться непосредственно - другими словами, сеть процессоров изоморфна графу расположения регионов. Таким образом, каждый процессор может проанализировать информацию, хранящуюся в соседних процессорах и на соответствующих им дугах, и принять решение о возможности слияния. Следует отметить, что, когда слияние осуществляется параллельно, решение о слиянии должно быть согласовано обоими процессорами; если разрешить принимать решение о слиянии регионов самостоятельно, то можно обнаружить, что регион А объединяется с регионом В и в то же время регион В объединяется с регионом С, что ведет к несостоятельности (имеются новые узлы, представляющие А+В и Б + С, но нет узла Л+2? +С, что в любом случае не является правильным слиянием). Для устранения этого следует разрешать слияние только несвязанных пар. Дополнительные сведения по параллельной обработке регионов можно найти в работе [18]. 24.4. ЗАКЛЮЧЕНИЕ В данной главе рассмотрены некоторые основные типы операций, используемых в обработке и анализе изображений как на уровне элементов растра, так и регионов, а также описаны идеализированные конфигурации многопроцессорных систем пригодных для параллельного выполнения таких операций. Показано, что для операций на уровне элементов, преобразующих изображение в изображение, наиболее естественной является ячеечная матричная архитектура, при которой процессоры объединены в регулярную решетку. С другой стороны, при измерении характеристик изображений наибольшая эффективность может быть достигнута при использовании древовидной структуры соединений, в которой процессоры расположены в позициях листьев дерева. Для параллельной обработки регионов, определенных кодами границ, пригодна кольцевая структура многопроцессорной системы. Если регионы определены наибольшими блоками, например кодами длин проходов или квадродеревом, то удобны другие схемы соединений. На более абстрактных уровнях, когда регионы определены списками характеристик, слияние регионов может выполняться параллельно при использовании сети процессоров, связанных в соответствии с графом расположения регионов. Параллельная обработка на уровне регионов требует, как правило, гораздо меньшего числа процессоров, чем параллельная обработка на уровне элементов растра. В состав ячеечной матричной машины для параллельной обработки изображения размером 512X512 при ее конфигурации "процессор на элемент изображения" должно входить около 1/4 миллиона процессоров, что на практике пока невозможно, в то время как обработка на уровне регионов требует всего нескольких сотен процессоров на регион (в зависимости от их сложности) или даже нескольких процессоров - при обработке графа связи регионов в зависимости от сложности разбиения. Такое число процессоров в системе вполне допустимо, но организация их связи представляет проблему. При обработке на уровне элементов растра обрабатываемые изображения всегда будут одного и того же размера, и соединения с соседями остаются одними и теми же для различных изображений, поэтому такая ячеечная матричная машина может быть построена раз и навсегда. Напротив, при обработке на уровне регионов соединения меняются от образа к образу, поскольку формы регионов нельзя предсказать заранее. Хуже того, может потребоваться изменять соединения в ходе вычислений по мере того, как вводятся новые регионы или сливаются старые. Это требует некоторого типа реконфигурируемой многопроцессорной архитектуры [19], в которой реконфигурация сама должна в идеале осуществляться параллельно. Для некоторых типов представлений (например, для представления в кодах границ, для которого могут использоваться связанные кольца процессоров) такая реконфигурация может быть относительно легкой; однако для других представлений, требующих древовидной графоподобной конфигурации соединений, параллельную реконфигурацию может оказаться не так просто реализовать таким образом, чтобы избежать узких мест в межпроцессорных соединениях. По мере того, как достижения в технологии произ- 0 ... 66 67 68 69 70 71 72 ... 78 |












