Раздел: Документация
0 ... 32 33 34 35 36 37 38 ... 290 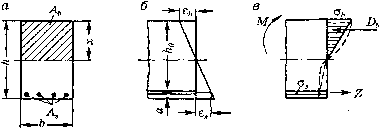 Рис. 3.6. Напряженно-деформированное состояние при изгибе при расчете по «классической теории»: а - армирование сечения; б - эпюра деформаций; в - эпюра напряжений Принимается справедливой гипотеза плоских сечений. Таким образом, здесь пренебрегают искривлением сечений, которое возникает вследствие влияния поперечных сил, неоднородности бетона, наличия двух материалов с совершенно различными упругими свойствами, усадки бетона, трещин в растянутой зоне и других причин. Модуль упругости бетона сжатой зоны принимается постоянным независимо от величины напряжений, и в расчет вводится нормированное постоянное для данной прочности бетона число а = EJЕь. При определении напряжений считают, что деформации пропорциональны напряжениям, т.е. принимается закон Гука, но при различных модулях упругости при сжатии и растяжении. Иначе говоря, эпюры напряжений в сжатой и растянутой зонах ограничены прямыми линиями, имеющими различный уклон. Для применения формул сопротивления материалов железобетонное сечение преобразуют в эквивалентное в статическом отношении однородное сечение, приведенное к бетону. Вследствие совместности работы бетона и арматуры и сцепления между ними деформации арматуры и бетона одинаковы, т.е. ts= гь; следовательно, as IEs ~ аь IЕь, откуда os=EsobIEb=aob.(3.21) Это означает, что каждую единицу площади сечения арматуры можно условно приравнять к а единицам площади бетона. Площадь приведенного сечения железобетонного элемента, показанного, например, на рис. 3.6, будет АгЫ = Ah + aAs = bx + aAs.(3.22) Момент инерции того же приведенного сечения относительно нейтральной оси (пренебрегаем ввиду малости моментов инерции арматуры относительно собственной оси) JreJ=bxi/Ъ + аАХК-х)1. Напряжения в бетоне и арматуре определяют по формулам сопротивления материалов: ob = Мх 11гЫ; а, = М (h0 - х) / . Высоту сжатой зоны х определяют из, условия, что статический момент приведенного сечения относительно нейтральной оси равен нулю: Sred = bx212 - aAs (h0 - x) = 0. Метод расчета по допускаемым напряжениям имеет ряд серьезных недостатков. Во-первых, в стадии II эпюра сжимающих напряжений в бетоне не треугольная, а криволинейного очертания. Во-вторых, число а, вводимое в расчет, не постоянно, а зависит от величины напряжений в бетоне, состава, возраста, прочности бетона и других факторов. Сопоставление расчетных величин с результатами опытов показало, что напряжения в арматуре железобетонных элементов, полученные из расчета, всегда больше действительных, что приводит к перерасходу стали, причем изменение числа а незначительно отражается на величине напряжения в арматуре. Напряжения же в бетоне в зависимости от принятого числа а могут быть как больше, так и меньше действительных. Таким образом, этот метод не только не позволяет определить действительные напряжения в бетоне и арматуре, но и не дает также возможности спроектировать конструкцию с заранее заданным запасом прочности. 3.5.2. Расчет по разрушающим усилиям В основу метода положены следующие положения. 1. Расчет производится по стадии III напряженного состояния элемента, т.е. по стадии разрушения; соответственно в расчетные формулы вводятся: для бетона - предел прочности на сжатие при изгибе; для арматуры - предел текучести (временное сопротивление) стали. Работа бетона на растяжение не учитывается, так как на стадии III бетон в растянутой зоне из работы выключается. 2.Эпюра напряжений в сжатой зоне бетона изгибаемых элементов принимается прямоугольной вместо действительной криволинейной. При незначительной погрешности расчета (до 2%) это приводит к существенному упрощению формул. 3.При принятых предпосылках, исходя из условий равновесия в момент, предшествующий разрушению, определяются разрушающие усилия. Усилие, действующее в сечении элемента, должно быть не более допускаемого, определяемого как частное от деления величины разрушающего усилия на коэффициент запаса прочности/С, т.е. М < Ми! К, N <Nul К. В этом методе расчета остаются неизвестными напряжения в бетоне и арматуре при эксплуатационной нагрузке, но зато становится известным коэффициент запаса прочности, что значительно важнее. Отпадает надобность в гипотезе плоских сечений, модулях упругости материалов и числе а. Расчетом по разрушающим усилиям учитываются упругопластичес-кие свойства железобетона, правильнее отражается работа железобетона под нагрузкой. Благодаря более полному использованию работы арматуры достигается существенная экономия металла по сравнению с расчетом по допускаемым напряжениям. Недостаток метода состоит в том, что невозможен учет изменчивости нагрузок и прочностных характеристик материалов при едином общем коэффициенте запаса прочности. 3.6. Расчет по предельным состояниям При расчете железобетонных конструкций по первой группе предельных состояний - по несущей способности - предельное состояние определяют так же, как и при расчете по разрушающим усилиям, т.е. по стадии III напряженного состояния. Однако расчетная несущая способность определяется в зависимости от системы коэффициентов: надежности по нагрузке, по бетону и арматуре, условий работы материалов и конструкций и др., что позволяет изменчивость свойств материалов, значений нагрузок и влияние различных факторов учитывать дифференцированно. Это приводит к более полному учету различных особенностей как самих конструкций, так и условий их эксплуатации и возведения. 0 ... 32 33 34 35 36 37 38 ... 290 |












