Раздел: Документация
0 ... 29 30 31 32 33 34 35 ... 290 3.3. Напряжения и деформации железобетона при растяжении При осевом растяжении железобетонного элемента различают три характерные стадии напряженно-деформированного состояния. В стадии I напряженно-деформированного состояния в элементе нет трещин, напряжения в бетоне аы < Ru и одинаковы во всех сечениях (рис. 3.2). Деформации бетона и арматуры равны по всей длине элемента, так как сцепление между ними не нарушено: £s = Еы = °ы IК = аы lv,E„.(3.5) Напряжения в арматуре о", = £А = °ь£, /i7A = аъ,а vt (3.6) По мере увеличения нагрузки наступает конечный этап стадии I, предшествующий образованию трещин в бетоне. Напряжения в бетоне достигают предела прочности на растяжение, а деформации, согласно формуле (3.5), - величины еы = Rbt lv,Eb. На основании опытов можно принять v, =0,5, тогда еы =2ЯЫ/ЕЬ, а напряжения в арматуре os = Rh,alv, = 2aRbl.(3.7) 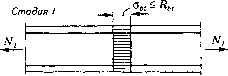 Стадия IIТрещины 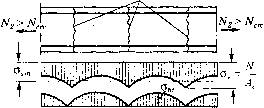 Рис. 3.2. Напряженное состояние при осевом растяжении Усилие, вызывающее появление трещин, будет равно сумме уси- лий в бетоне и арматуре: NM = RbA+laRbA, = Rbl(A+2aAs).(3.8) При дальнейшем увеличении нагрузки в бетоне появляются трещины, наступает стадия II напряженно-деформированного состояния, при которой в сечениях, проходящих через трещины, сопротивление растяжению оказывает только арматура, а в сечениях между трещинами - арматура и бетон. По мере удаления от трещин напряжения в арматуре убывают, а в бетоне возрастают, так как в работу включается бетон, расположенный на участке между трещинами, в пределах которого сцепление с арматурой остается ненарушенным. Для учета работы бетона на участках между трещинами, по предложению В.И. Мурашева, вводится коэффициент \\ts, представляющий собой отношение средних напряжений а„„(или деформаций esm) в арматуре на участке между трещинами к напряжениям (или деформациям е5) в сечениях с трещинами: - - -(3.9) Зависимость между напряжениями и деформациями в арматуре на участке между трещинами можно представить в следующем виде: cs=£sEs=Es=esmEsm,(ЗЛ0) где Esm = -?-- средний модуль упругости растянутой арматуры с уче- У S том работы бетона между трещинами. На рис. 3.3 показан график зависимости деформаций от напряжений в арматуре с учетом работы растянутого бетона и при удлинении свободного металла. Средний модуль упругости арматуры Ет графически представляет собой тангенс угла наклона секущей в точке с заданным напряжением, т.е. с, Е„ = - tga„.
Рис. 5.5. Зависимость деформаций арматуры от напряжений при растяжении железобетонного элемента В стадии III напряжения в арматуре достигают временного сопротивления ои и железобетонный элемент разрушается при усилии N = A,-ou. 3.4. Напряжения и деформации железобетона при изгибе При изгибе железобетонной балки в зависимости от величины изгибающего момента в сечениях последовательно возникают различные стадии напряженно-деформированного состояния. Стадия I. При малых нагрузках (изгибающих моментах) напряжения в бетоне и арматуре малы, в бетоне развиваются преимущественно упругие деформации. Эпюры напряжений в сжатой и растянутой зонах почти прямолинейны (рис. 3.4, а). При увеличении нагрузки напряжения в бетоне и арматуре возрастают, в бетоне развиваются как упругие, так и неупругие деформации, эпюры напряжений слабо искривляются, нейтральная ось балки перемещается в сторону сжатой грани балки. Стадия I характеризуется отсутствием трещин в растянутом бетоне и усилия воспринимаются всем сечением. При определении напряже- 0 ... 29 30 31 32 33 34 35 ... 290 |
||||||||||||||||||












