Раздел: Документация
0 ... 28 29 30 31 32 33 34 ... 290 Напряжения и деформации железобетона. Методы расчета прочности 3.1. О теории сопротивления железобетона Зависимость между напряжениями и деформациями бетона нелинейна. Армирование не устраняет этой особенности работы бетона под нагрузкой. Поэтому теория сопротивления упругих материалов для железобетона непригодна. Такие свойства бетона и железобетона, как ползучесть, усадка, образование трещин в растянутой зоне железобетонных элементов, существенно влияет на напряженно-деформированное состояние железобетонных конструкций. Если, кроме того, учесть, что эти свойства в значительной степени зависят от вида бетона и арматуры, характера армирования, вида напряженного состояния, возраста бетона, длительности действия нагрузки и других факторов, то станет понятным, насколько сложна задача создания строгой теории сопротивления железобетона. Все вопросы, связанные с сопротивлением бетона и железобетона, могут быть решены только на основе опытных данных, поэтому результаты экспериментальных исследований в создании теории железобетона имеет исключительное значение. В процессе развития и усовершенствования теории расчета железобетонных элементов по несущей способности пройдены три основных этапа. На первом этапе для расчета железобетонных элементов пользовались теорией упругости железобетона (расчет по допускаемым напряжениям), основанной на формулах сопротивления материалов, прини- мая, что сечения железобетонных элементов работают в упругой стадии. На втором этапе, в 1931 г. (предложение А.Ф. Лолейта), под руководством А. А. Гвоздева были получены важные данные, позволившие осуществить более прогрессивный метод расчета по стадии разрушения, который послужил основой норм и технических условий проектирования железобетонных конструкций, действовавших в период с 1938 по 1955 г. На третьем этапе, с 1955 г., был принят новый метод расчета - по расчетным предельным состояниям, который положен в основу современных методов расчета и проектирования строительных конструкций, в том числе бетонных и железобетонных. Этот метод постоянно совершенствуется. 3.2. Напряжения и деформации железобетона при сжатии Железобетонные элементы, подвергаемые осевому сжатию (рис. 3.1), армируют в основном продольными и поперечными стержнями (хомутами). Последние имеют двоякое назначение: препятствуют выпучиванию продольной арматуры при сжатии и обеспечивают соединение от-дельныхпродольных стержней в плоские и пространственные каркасы. При осевом сжатии железобетонных элементов деформации в арматуре и прилегающем слое бетона равны и могут быть выражены через напряжения (см. 2.1.3): = о, IE, =еь = аь/Е„ = аь lvEb.(3.1) 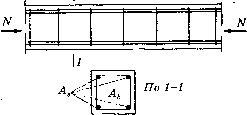 Рис. 3.1. Осевое сжатие железобетонного элемента 4. Строит, констр. Уч. пос. Уравнение (3.1) представляет собой условие совместности деформаций арматуры и бетона. С другой стороны, из условия равновесия элемента можно составить уравнение, выражающее равенство между внешним усилием и внутренними усилиями, действующими в бетоне и в продольной арматуре: N = crbA+cysAs,(3.2) где As - площадь сечения продольной арматуры; Л - площадь сечения бетона. Из (3.1) получим напряжение в арматуре o,=obE,lvEb = abalv,(3.3) где a-EJEb - коэффициент приведения. Подставляя формулу (3.3) в (3.2), получим: N = abA+abaAs/v = abA(l+a/x/v),(3.4) откуда N аь =--, A(l + ajx/v) где \i = AJА - коэффициент армирования. Напряжения в бетоне и арматуре зависят от коэффициента упругости v , который связан с напряжением нелинейной зависимостью. Кроме того, коэффициент v при длительном выдерживании элемента под нагрузкой вследствие развития деформаций ползучести уменьшается, что приводит к снижению напряжений в бетоне. При этом напряжения в арматуре, как следует из условия (3.2), должны возрастать. Таким образом, с течением времени происходит перераспределение внутренних усилий между бетоном и арматурой. При увеличении внешней нагрузки напряжения в бетоне достигают предела прочности при сжатии Rb, а в арматуре, согласно формуле (3.3), - величиныas= Ri,alv = 4аЛь, так как при разрушении v = 0,25. Из выражения (3.3) следует, что предельные напряжения в арматуре перед разрушением железобетонных элементов, подвергаемых сжатию, зависят не только от механических свойств стали, но и от упругопласти-ческих свойств бетона, что учитывается при установлении расчетного сопротивления арматуры сжатию. 0 ... 28 29 30 31 32 33 34 ... 290 |












