Раздел: Документация
0 ... 59 60 61 62 63 64 65 ... 290 Косой изгиб и косое внецентренное сжатие Косой изгиб имеет место, когда плоскость изгибающего момента (или плоскость действия внешней нагрузки и реакций, расположенных в той же плоскости) не совпадает ни с одной из главных плоскостей, проходящих через главные оси инерции сечения элемента. Если опорные устройства элемента таковы, что способны воспринимать крутящий момент (например, при жестком защемлении концов элемента) и плоскость внешней нагрузки не проходит через центральную продольную ось элемента, то косой изгиб будет происходить совместно с кручением. При отсутствии последнего в элементах из упругих материалов нормальные напряжения (рис. 7.1) где Мх = М cos Р ; Му = М sin /3 . Уравнение нулевой линии получим из условия М М -z-x---у = 0. Эта линия проходит через начало координат, которое в общем случае может не совпадать с центром тяжести сечения. Угол ее наклона определяется из выражения ст = ± (7.1) х МУ /, A/sin/j /, /,. = -tg/3, (7.2) у Мх Ix Mcos/3 1Х 1Х а 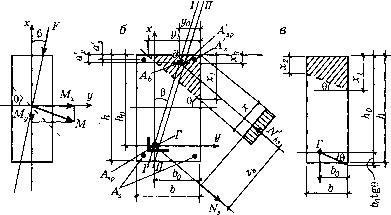 Рис. ,7.1. К расчету железобетонных элементов с сосредоточенным армированием на косой изгиб: а - положение силовой плоскости и нейтральной линии в элементах из упругих материалов; б - схема действующих усилий в железобетонном элементе; в - к определению размеров сжатой зоны сечения откуда следует, что при косом изгибе нулевая линия не перпендикулярна к силовой линии. При 1у > 1Х угол в > Р . В железобетонном элементе вследствие неупругой работы бетона и трещин в растянутой зоне нейтральная ось перед разрушением перемещается и располагается к наиболее сжатому волокну ближе, чем в элементе из упругих материала (рис. 1Л,б). Плоскость I-I внутренней пары сил в общем может не совпадать с плоскостью П-П действия внешней нагрузки, но обязательно ей параллельна. Положение плоскости I-I в основном определяется армированием растянутой зоны. Эта плоскость проходит через точку приложения равнодействующей усилий арматуры растянутой зоны Ns (в которой располагается начало координат осей* - у) параллельно силовой плоскости П-П. Точка приложения равнодействующей сжатой зоны Nb! должна также лежать на следе плоскости I-I, что при заданном армировании сжатой зоны определяет площадь/!;, этой зоны и выеотух. В элементах прямоугольного сечения сжатая зона может иметь форму треугольника или трапеции (приу7>£). Прочность косоизгибаемого элемента по нормальному сечению проверяют в плоскости перпендикулярной линии, ограничивающей сжатую зону. При армировании, сосредоточенном около сжатой и растянутой граней и первом случае расчета (£ < %R) условия прочности получают из уравнения моментов относительно оси, проходящей через точку «Г» (см. рис. 7.1,6) приложения равнодействующей усилий в арматуре растянутой зоны. Mcos(e-)(RbA+RsA+c4PK-(7.3) Площадь сжатой зоны Аь определяют из уравнения равновесия ГЛЛр + RA = RbA + + °sA -(7.4) Отношение моментов c = My/Mx=Ns(b0-y0)/Ns(h0-x0) = (b0-y0)/(hQ-x0), (7.5) где х0 и у0 - расстояния от точки приложения равнодействующей усилий в сжатой зоне до сжатых граней (см. рис. 7.1, б). При отсутствии арматуры в сжатой зоне, т.е. при А[ = Asp = 0 , два последних члена уравнения (7.4) отпадут. Подставляя (7.5) в (7.4) и имея в виду, что в этом случае Аь = 0,5х,у; х0 =0,33*, и у0 = 0,33у,, получим уравнение +3-2+с=0,(7.6) из которого определяется х1; а затем из уравнения (7.4) - у}. Если Х\ окажется отрицательным или ji>b, то это будет означать, что сжатая зона имеет форму трапеции. В практике такой случай встречается редко. При трапециевидной форме сжатой зоны (рис. 7.1, е) ее размерыXj и х2 могут быть определены аналогичным образом. В этом случае правая часть уравнения (7.4) примет вид 0,5(х, +x2)bRb, а в равенстве (7.5) значения х0 и у0 определяются из следующих выражений: х0 = (l/3)(x,2 +х,х2 + х2)/(х, +х2) ; у0 = (b 13)(х, + 2х2) /(х, + х2) . В результате получим уравнение 0 ... 59 60 61 62 63 64 65 ... 290 |












