Раздел: Документация
0 ... 5 6 7 8 9 10 11 ... 39 3 Как следует из названия АЛУ, ко- ЛОГИЧЕСКИЕ ОПЕРАЦИИ торое является одним из основных функциональных блоков микрокомпьютера, оно предназначено для выполнения не только арифметических, но и логических операций. При вычислении значений логических функций процессор использует правила логической алгебры (ее часто называют по имени ее изобретателя, английского математика Дж. Буля, булевой алгеброй). В булевой алгебре, основанной на двузначной логике, все переменные могут принимать одно из двух значений - «истинно» или «ложно» (аналогично цифрам двоичного числа, их обычно обозначают символами «1» или «О» соответственно). Число основных логических операций (как и арифметических действий) равно 4. Это логическое сложение «ИЛИ», логическое умножение «И», отрицание «НЕ» и «Исключающее ИЛИ». Давайте познакомимся со свойствами этих четырех логических операций и рассмотрим примеры их использования. Логическое сложение (ИЛИ) Операция логического сложения обозначается знаком «+» (или «v»). Несмотря на кажущееся сходство, следует отличать обозначение логической операции от знака «+», используемого при арифметическом сложении (во избежание недоразумений рекомендуется там, где есть вероятность перепутать эти две операции, использовать только обозначение «v»). Результат логического сложения можно представить в виде следующего правила: Если хоть одно из слагаемых равно «1», то в результате также получится «1» Рассмотрим конкретный пример. Пусть переменная X обозначает следующее: в комнате находится человек (если находится, то значение функции равно «1», если нет - «О»). Эту переменную можно представить в виде суммы двух переменных - А (в комнате находится мужчина) и В (в комнате находится женщина). Тогда в трех случаях из четырех значение логической функции X = А + В равно «1», и только в одном случае оно равно «О». На Рис. 3.8 приведена таблица истинности для операции логического сложения.  «ИЛИ» А + В = ХилиАуВ = Х Таблица истинности операции «ИЛИ»
Рис. 3.8. Таблица истинности для операции логического сложения Логическое сложение часто используется при обработке двоичных чисел. Например, если требуется заменить на «1» только первый разряд 8-разрядного двоичного числа X (эта операция называется установкой значения разряда), то для этого в каждом разряде числа X выполняется операция логического сложения с соответствующими значащими цифрами двоичного числа 00000010, как показано на Рис. 3.9. Установка разряда 8-разрядное число Производим поразрядное сложение > Мы хотим установить«1»только в 1-м разряде Обратите внимание: 10 110 1 + + + + + + 0 0 0 0 0 0 1 0 1 1 0 1 □ 1 Результат вычисления функции «ИЛИ» не совпадает с результатом арифметического сложения А ( Установленный разряд Рис. 3.9. Установка разряда методом логического сложения 3~2э70 г Логическое умножение (И) Логическое умножение обозначается знаком «» (или «л»). Результат логического умножения можно определить с помощью следующего правила: Результат равен «1» только в том случае, если оба множителя равны «1» Таблица истинности для операции логического умножения представлена на Рис. 3.10. Эту таблицу легко запомнить, так как результат при логическом умножении тот же, что и при арифметическом умножении двоичных цифр. Если в рассмотренном выше примере оставить прежним смысловое значение введенных логических переменных А и В, то смысл логической переменной Y, равной произведению А • В, выражается в виде утверждения: «в комнате одновременно находятся мужчина и женщина». «И» А- В = Х или АлВ = Х Таблица истинности операции «И»
Рис. 3.10. Таблица истинности операции логического умножения При обработке двоичных чисел логическое умножение используется, например, когда нам нужно выборочно обнулить разряды 8-разрядного двоичного числа, оставив значения остальных разрядов прежними. В этом случае выполняем логическое умножение на 1 в тех разрядах, значения которых мы хотим сохранить, а над значащими цифрами остальных разрядов производим логическое умножение на 0 (Рис. 3.11). Такая операция называется маской разряда. Аналогично можно обнулить только один из разрядов двоичного числа. Пример такой операции приведен на Рис. 3.12. Маска разряда 8-разрядное число 10 110 Производим поразрядное логическое умножение У Сохраняем прежнее значение - только в 1-м разряде Результат вычисления 0 0 0 0 0 1 0 0 0 о о о о о [Т]о о Остальные разряды обнуляются 7v. Значение, которое требуется сохранить Рис. 3.11. Маскирование разряда путем логического умножения Обнуление разряда 8-разрядное число Производим поразрядное логическое умножение У Во всех разрядах «1», кроме обнуляемого разряда Результат операции -
10 1 1 0 0 1 о Содержимое других разрядов не изменяется Операция обнуления разряда выполнена Рис. 3.12. Обнуление разряда путем логического умножения Отрицание (НЕ) Операция отрицания изменяет значение логической переменной На противоположное. Она изображается чертой, расположенной над обозначением переменной. Например, выражение А= X означает, что X является отрицанием А. Правило, по которому осуществляется операция отрицания, может быть сформулировано в следующем виде: При отрицании «О» и «1» взаимно заменяют друг друга (происходит инверсия значений логических переменных) На Рис. 3.13 представлена таблица истинности для логической операции отрицания. Черточки над выводами MREQ, IORQ, RD (Рис. 2.4) во второй главе, посвященной описанию функций выводов процессора Z80, обозначают инверсию (отрицание) логического сигнала. Отрицание используется при вычислении дополнительного кода двоичного числа. «НЕ» А = Х Таблица истинности операции «НЕ»
Рис. 3.13. Таблица истинности логической операции отрицания Исключающее ИЛИ В качестве обозначения операции «Исключающее ИЛИ» используется знак + (или V). Результат этой логической операции можно определить по правилу: Результат равен «1» только в том случае, если значения переменных противоположны Таблица истинности операции «Исключающее ИЛИ» приведена на Рис. 3.14. Рассмотрим на конкретном примере смысл этой операции. Предположим, что господин К и господин N внесены в список кандидатов на пост президента. Переменной А обозначим событие: «господин К наберет больше половины голосов избирателей», а переменной В: «господин N наберет больше половины голосов избирателей». Тогда событие X: «второго тура голосования не потребуется» является результатом операции «Исключающее ИЛИ» над переменными А и В . Исключающее ИЛИ АФВ = Х или AV В = X Таблица истинности операции «Исключающее ИЛИ»
Рис. 3.14. Таблица истинности операции «Исключающее ИЛИ» Операция «Исключающее ИЛИ» используется, например, если требуется инвертировать содержимое некоторого разряда 8-разрядного числа (Рис. 3.15). Для этого мы применяем операцию «Исключающее ИЛИ» над значащей цифрой разряда, который мы хотим инвертировать, и единицей. Кроме того, в результате применения этой операции ко всем разрядам двух одинаковых 8-разрядных чисел получается число, все разряды которого равны 0. Это означает, что операцию «Исключающее ИЛИ» можно использовать для очистки (обнуления) регистра. Инвертирование разрядов -разрядное число 0 10 1 Производим поразрядно операцию «Исключающее ИЛИ». Мы хотим инвертировать только 4 младших разряда Результат вычисления 0 0 0 0 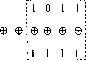 0 10 10 о о Содержимое не меняется Инвертировано Рис. 3.15. Пример применения операции «Исключающее ИЛИ» 0 ... 5 6 7 8 9 10 11 ... 39 |












